یکی از اتحادهای مهم و جدید جبری در کتاب نظام جدید، اتحاد مربع سه جمله ای است. در این مقاله فیلم آموزشی آن توسط تیم سایت تدریس خصوصی استادلینک برای شما عزیزان تهیه شده است.
استادلینک سایت جستجوی آنلاین معلم و مشاور خصوصی بوده که شما با مراجعه به صفحۀ اصلی سایت استادلینک، می توانید لیست بهترین اساتید را همراه با رزومه، سوابق کاری، فیلم نمونه تدریس و نظر شاگردان قبلی او را مشاهده نمایید و به صورت مستقیم با استاد موردنظرتان ارتباط بگیرید.
همچنین می توانید از طریق پشتیبانی واتساپ سایت استادلینک، اقدام به رزرو معلم خصوصی خود نمایید. برای این کار روی آیکون واتساپ ضربه بزنید.
فیلم آموزش اتحاد مربع سه جمله ای
آموزش ویدیویی اتحاد مربع سه جمله ای توسط تیم اساتید ریاضی سایت استادلینک برای شما عزیزان تهیه شده است.
جهت رزرو معلم خصوصی ریاضی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.
توضیحات فرمول اتحاد مربع سه جمله ای
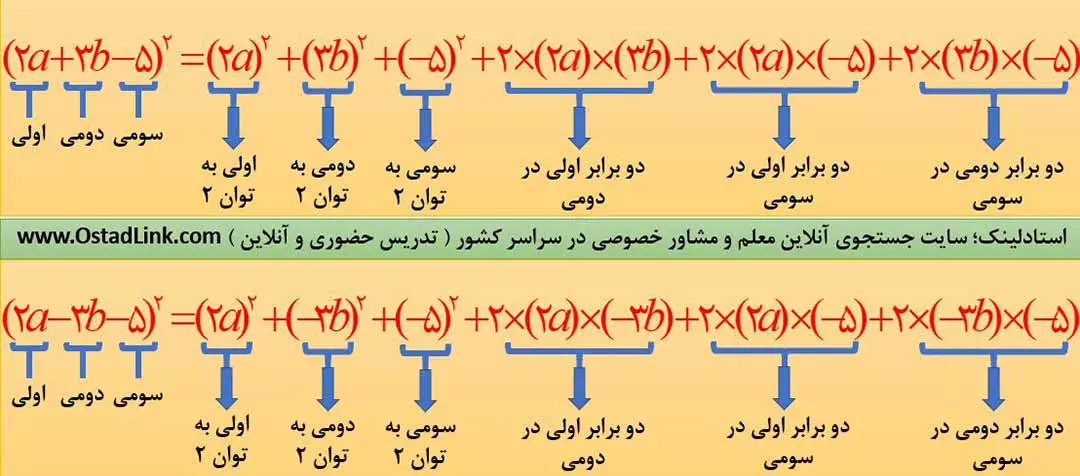
اتحاد مربع سه جمله ای، از یک پرانتز که داخل آن سه جملۀ غیر متشابه وجود دارد و کل پرانتز به توان دو رسیده، تشکیل شده است. این اتحاد در سالهای اخیر مورد توجه طراحان کنکور و طراحان آزمون های تیزهوشان و نمونه دولتی واقع شده است. فرمول کلی اتحاد مربع سه جمله ای را در تصویر زیر مشاهده نمایید.
توجه1: حتماً علامت جملات در موقع محاسبۀ اتحاد مربع سه جمله ای مورد توجه قرار گیرد.
توجه2: بهتر از مربع ( توان دوم ) برخی از اعداد را که در جدول زیر آمده است به خاطر بسپارید.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![\[ 3^2=9 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-876e624c794edc3453f68ef95a522700_l3.png "Rendered by QuickLaTeX.com")
![\[ 2^2=4 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-4f17ca07879b35008a6c6aa5f551f568_l3.png "Rendered by QuickLaTeX.com")
![\[ 1^2=1 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-cea808b52d420980174e611698b943f1_l3.png "Rendered by QuickLaTeX.com")
![\[ 0^2=0 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-8abb0228800f7a78353267e15ba625c5_l3.png "Rendered by QuickLaTeX.com")
![\[ 7^2=49 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-77232d98c1fe42eb7771dc83746d6b07_l3.png "Rendered by QuickLaTeX.com")
![\[ 6^2=36 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-d97b6869e105c7187a2e488800fd28e9_l3.png "Rendered by QuickLaTeX.com")
![\[ 5^2=25 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-c52e5840f56083580b7091f7130e9690_l3.png "Rendered by QuickLaTeX.com")
![\[ 4^2=16 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-e5bbffcbc641553e4a290e5b6963c0f9_l3.png "Rendered by QuickLaTeX.com")
![\[ 11^2=121 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-0cfd4e120e74db72b8eb51f92f4d3395_l3.png "Rendered by QuickLaTeX.com")
![\[ 10^2=100 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-c2ec283a9cab98e46bae8a2829e4c9d9_l3.png "Rendered by QuickLaTeX.com")
![\[ 9^2=81 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-6ec225b9e66a98861571a50535bdf94b_l3.png "Rendered by QuickLaTeX.com")
![\[ 8^2=64 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-5e82c243695ac15fe79e9503365f80fd_l3.png "Rendered by QuickLaTeX.com")
![\[ 15^2=225 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-60d99db7612e1cafc66b399605e77009_l3.png "Rendered by QuickLaTeX.com")
![\[ 14^2=196 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-c7aad52bdf62d4adee5d0c1856543e92_l3.png "Rendered by QuickLaTeX.com")
![\[ 13^2=169 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-51549c55ad0441a33e883f76ca4e26fc_l3.png "Rendered by QuickLaTeX.com")
![\[ 12^2=144 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-419d7fcd019bd79084e26bd7e19c7276_l3.png "Rendered by QuickLaTeX.com")
![\[ 19^2=361 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-f175bd66d11dd349e956aada0e14e477_l3.png "Rendered by QuickLaTeX.com")
![\[ 18^2=324 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-61f031bd4a39ad4a35f946652f4de205_l3.png "Rendered by QuickLaTeX.com")
![\[ 17^2=289 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-a7a1310b61ef411fa315334184746360_l3.png "Rendered by QuickLaTeX.com")
![\[ 16^2=256 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-ea39ad53113b1e6fe3dcc1a812acb730_l3.png "Rendered by QuickLaTeX.com")
![\[ 30^2=900 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-48d9c23573732e1c16ddb839ab80a236_l3.png "Rendered by QuickLaTeX.com")
![\[ 25^2=625 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-7b09728abb1c0df6fdbfc27f22034383_l3.png "Rendered by QuickLaTeX.com")
![\[ 21^2=441 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-a5d203af09e20aca896cd7e91bb5c4e8_l3.png "Rendered by QuickLaTeX.com")
![\[ 20^2=400 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-f4f55a9d67e762cec52a97aede6acc21_l3.png "Rendered by QuickLaTeX.com")
حل چند مثال از اتحاد مربع سه جمله ای
در تصویر زیر، چند مثال مهم از فرمول اتحاد مربع سه جمله ای برای شما عزیزان حل شده است.
اصطلاحات رایج در ریاضی
در این بخش با مفاهیم و اصطلاحات رایج در ریاضی آشنا می شویم. حتماً قبل از آشنایی با اتحادها و بخصوص اتحاد چاق و لاغر، این مفاهیم را مرور کنید.
- مربع = مجذور: مربع یا مجذور عدد x یعنی x2. به عبارت دیگر یعنی آن عبارت را به توان دوم برسانید یا دو بار در خودش ضرب کنید. به عنوام مثال، مربع یا مجذور 10، عدد 100 می شود.
- جذر = رادیکال: به عنوان مثال، جذر عدد 36، عدد 6 می شود. برخی اعداد مانند 36 جذر کامل دارند و برخی اغداد مانند 8، جذر کامل و درستی ندارند.
- ریشۀ دوم: تفاوت ریشۀ دوم و رادیکال در این است که در ریشۀ دوم، عدد حاصل شده هم با علامت مثبت و هم با علامت منفی بیان می شود. مثلاً ریشۀ دوم عدد 36، عدد 6+ و عدد 6- می شود در صورتی که جذر یا رادیکال 36، عدد 6 فقط می شود.
- مکعب: مکعیب عدد x یعنی x3. به عبارت دیگر آن عبارت را به توان 3 برسانید یا سه بار در خودش ضرب کنید. به عنوان مثال مکعب 5، عدد 125 می شود.
- کعب = رادیکال فرجۀ سه = ریشۀ سوم: همۀ اینها یک مفهوم دارند. به عنوان مثال کعب عدد 8، عدد 2 می شود. برخی اعداد مانند 8، ریشۀ سوم کامل دارند و برخی اعداد مانند ماندد 10، ریشۀ سوم کامل و درستی ندارند.
- جملات متشابه: جملاتی که حرف انگلیسی و توان آنها مانند هم است مانند 5x2 و 8x2. جملات متشابه با هم قابلیت جمع و تفریق دارند مثلاً 8x2+5x2=13x2 می شود. جملات غیز متشابه، نمی توانند با هم جمع شوند. به عنوان مثال دو جملۀ 5x2-8x را در نظر بگیرید. از این ساده تر دیگر نمی توان آنها را نوشت!
- مجموع مجذور: دو عدد x و y را در نظر بگیرید. مجموع مجذور یا مجموع مربع x و y را به صورت x2+y2 نمایش می دهند. (اول توان 2 بعداً جمع)
- مجذور مجموع: دو عدد x و y را در نظر بگیرید. مجذور مجموع یا مربع مجموع x و y را به صورت 2(x+y) نمایش می دهند. (اول جمع کن بعد حاصل را به توان 2 ببرد.)
- مجموع مکعب: دو عدد x و y را در نظر بگیرید. مجموع مکعب آنها به صورت x3+y3 است. (اول به توان 3 ببر و بعد حاصل ها را با هم جمع کن.)
- مکعب مجموع: دو عدد x و y را در نظر بگیرید. مکعب مجموع آنها به صورت 3(x+y) است. (اول جمع کن و بعد حاصل را به توان 3 ببرید.)
توجه: بهتر است مکعب اعدا زیر را به خاطر بسپارید.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![\[ 3^3=27 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-1813155dcd833700f4e3a8eeb3a27502_l3.png "Rendered by QuickLaTeX.com")
![\[ 2^3=8 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-4a7096744c23292a71dffe254b9196be_l3.png "Rendered by QuickLaTeX.com")
![\[ 1^3=1 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-9d2a2b9b1c372e148079e9e850ebcb3f_l3.png "Rendered by QuickLaTeX.com")
![\[ 0^3=0 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-9dea45097cdec4852ebbd0d5803a802c_l3.png "Rendered by QuickLaTeX.com")
![\[ 7^3=343 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-91a644157ab5b0d93f3f3ca0e724283e_l3.png "Rendered by QuickLaTeX.com")
![\[ 6^3=216 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-305ac453d3e4b98c339edfd20d7cbc0a_l3.png "Rendered by QuickLaTeX.com")
![\[ 5^3=125 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-984ebb658d4ab340c8f5f9d9782c8a11_l3.png "Rendered by QuickLaTeX.com")
![\[ 4^3=64 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-9e2c530e73b49e98134c57d3fa192d91_l3.png "Rendered by QuickLaTeX.com")
![\[ 11^3=1331 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-7d6b8405f357a4f607838cab0bcc66c6_l3.png "Rendered by QuickLaTeX.com")
![\[ 10^3=1000 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-a2955772e7f262cb90684181f0e37d76_l3.png "Rendered by QuickLaTeX.com")
![\[ 9^3=729 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-f70e6471eaddd87494eb31c3b22a15e4_l3.png "Rendered by QuickLaTeX.com")
![\[ 8^3=512 \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-4719da5274c9eee1b8b1d30289b4dc91_l3.png "Rendered by QuickLaTeX.com")
تمرین در خانه ( Home Work ):
حاصل عبارت های زیر را به کمک اتحاد مربع سه جمله ای بدست آورده و پاسخ آنرا در بخش دیدگاه در پایین همین صفحه تایپ نمایید.
|
|
|
|
|
|
![\[ \left(2x-3y-5z^3\right)^2=? \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-e412fffb3a81a3b95169a01c14226d88_l3.png "Rendered by QuickLaTeX.com")
![\[ \left(2x-3y+5\right)^2=? \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-2967222a9573c4bb75eab24539370305_l3.png "Rendered by QuickLaTeX.com")
![\[ \left(\sqrt{x}+3\sqrt{y}+z\right)^2=? \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-4af4be54a7666cd34421b21e293bc4cd_l3.png "Rendered by QuickLaTeX.com")
![\[ \left(\sqrt{x}+3y-5z\right)^2=? \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-ec73e9ce67dffd86b9828bed4beadfdb_l3.png "Rendered by QuickLaTeX.com")
مقالات مرتبط:
آموزش ویدیویی اتحاد مربع دو جمله ای
آموزش ویدیویی اتحاد مکعب دو جمله ای
4 پاسخ
سلام
ممنون از سایت خوبتون
از شما معلم خصوصی ریاضی گرفتم واقعا راضی هستم
لطفا نحوه تجزیه اتحاد هارا هم قرار دهید
درود بر شما
از اینکه سایت جستجوی معلم خصوصی استادلینک را انتخاب نموده اید بسیار خرسندیم
عبارت ( آموزش تجزیه عبارت های جبری سایت استادلینک ) را در گوگل سرچ کنید و از طریق سایت استادلینک مشاهده نمایید.
درود بر شما
از اینکه سایت تدریس خصوصی استادلینک را انتخاب نموده اید بسیار خرسندیم
داخل گوگل سرچ کنید ( تجزیه عبارت های جبری استادلینک ) و وارد سایت استادلینک شده و تدریس تجزیه را مشاهده کنید.
لطفا سایت استادلینک را به دوستان خود معرفی نمایید.
http://www.OstadLink.com