در این مقاله و این فیلم آموزشی انیمیشنی، با انواع روش های تجزیه عبارت های جبری به کمک فاکتورگیری، اتحادها و روش ترکیبی آنها آشنا خواهید شد.
استادلینک؛ جامع ترین سایت جستجوی آنلاین معلم و مشاور خصوصی در سراسر کشور بوده (تدریس حضوری و آنلاین ) که با مراجعه به صفحه اصلی سایت استادلینک، لیست بهترین معلم خصوصی ریاضی کشور و همچنین فیلم نمونه تدریس و رزومه هر استاد را مشاهده کرده و به صورت مستقیم با آنها ارتباط بگیرید.
فیلم آموزشی تجزیه عبارت های جبری
جهت رزرو معلم خصوصی ریاضی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.
دانلود نمونه سوالات تجزیه عبارت های جبری
این سوالات از کتاب های ریاضی سال نهم تا دوازدهم برای شما گردآوری شده و حل تمامی آنها به همۀ دانش آموزان توصیه می شود.
| دانلود سوالات امتحانی تجزیه عبارت های جبری |
کاربرد تجزیه عبارت های جبری
جهت رزرو معلم خصوصی ریاضی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.
تجزیه عبارت های جبری، یعنی تبدیل عبارت های جبری به صورت ضرب دو یا چند پرانتز است. از تجزیه عبارت های جبری برای ساده سازی عبارت های گویا، مخرج مشترک گرفتن در عبارت های گویا و حل معادلات و … استفاده می شود.
روش های تجزیه عبارت های جبری
به طور کلی سه روش برای تجزیه عبارت های جبری وحود دارد که در فیلم به صورت مفصل و با حل مثال به آنها اشاره شده است:
- تجزیه عبارت های جبری به کمک فاکتورگیری
- تجزیه عبارت های جبری به کمک اتحاد ها
- تجزیه عبارت های جبری به روش ترکیبی ( اول فاکتورگیری بعد اتحاد )
یادآوری انواع اتحادها
جهت رزرو معلم خصوصی ریاضی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.
1- اتحاد مربع دو جمله ای
![\[{\left(a\pm b\right)}^2=a^2\pm 2ab+b^2\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-c88f689a22aaeae6f5def671312c007f_l3.png "Rendered by QuickLaTeX.com")
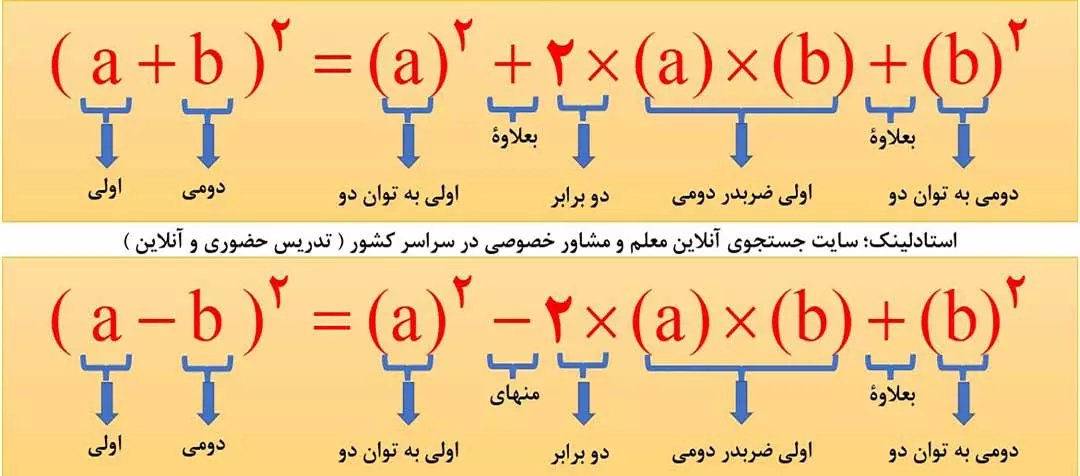
برای مشاهده فیلم آموزشی اتحاد مربع دو جمله ای، اینجا ضربه بزنید.
2- اتحاد مربع سه جمله ای
![\[{\left(a+b+c\right)}^2=a^2+b^2+c^2+2ab+2ac+2bc\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-adc44b13015fadfe0a00abceed50d78b_l3.png "Rendered by QuickLaTeX.com")
برای مشاهده فیلم آموزشی اتحاد مربع سه جمله ای، اینجا ضربه بزنید.
3- اتحاد مکعب دو جمله ای
![\[{\left(a\pm b\right)}^3=a^3\pm 3a^2b+3ab^2\pm b^3\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-fbea0977f84974035de15eb69c0ef98c_l3.png "Rendered by QuickLaTeX.com")
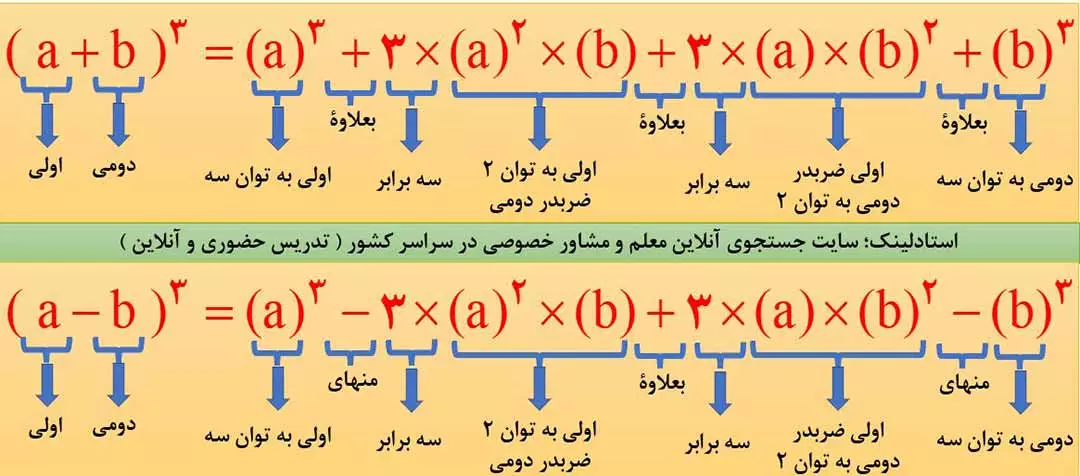
برای مشاهده فیلم آموزشی اتحاد مکعب دو جمله ای، اینجا ضربه بزنید.
4- اتحاد مزدوج
![\[\left(a-b\right).\left(a+b\right)=a^2-b^2\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-51c082b0393da2788d4c7d4aa333b7d0_l3.png "Rendered by QuickLaTeX.com")
برای مشاهده فیلم آموزشی اتحاد مزدوج، اینجا ضربه بزنید.
5- اتحاد چاق و لاغر
نام دیگر این اتحاد، اتحاد فیل و فنجون می باشد.
![\[\left(a\pm b\right).\left(a^2\mp ab+b^{2\ }\right)=a^3\pm b^3\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-e1ef684d4bada44de06574497b01860f_l3.png "Rendered by QuickLaTeX.com")
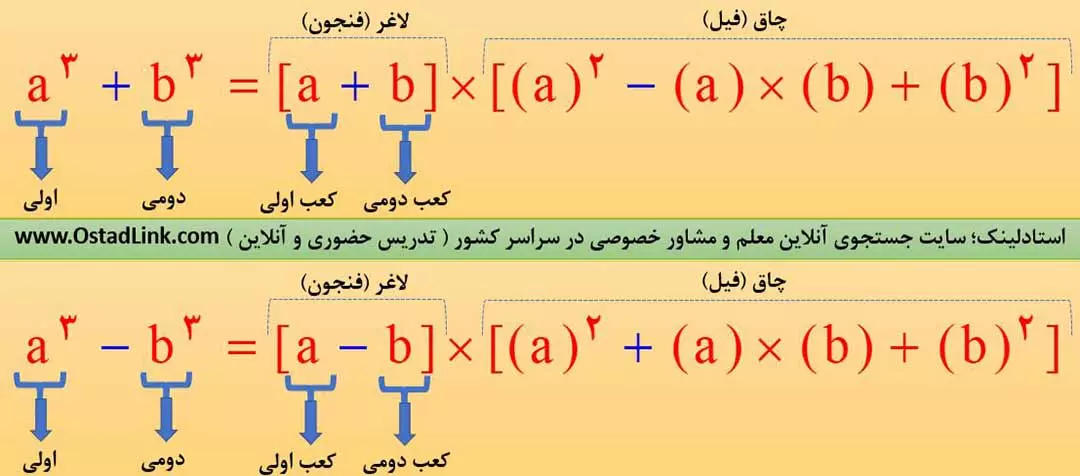
برای مشاهده فیلم آموزشی اتحاد چاق و لاغر، اینجا ضربه بزنید.
6- اتحاد یک جمله مشترک
![\[\left(x+a\right).\left(x+b\right)=x^2+\left(a+b\right)x+ab\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-c3ee470875a41ec056f91213aca3a986_l3.png "Rendered by QuickLaTeX.com")
برای مشاهده فیلم آموزشی اتحاد یک جمله مشترک، اینجا ضربه بزنید.
اصطلاحات رایج در ریاضی
در این بخش با مفاهیم و اصطلاحات رایج در ریاضی آشنا می شویم.
- مربع = مجذور: مربع یا مجذور عدد x یعنی x2. به عبارت دیگر یعنی آن عبارت را به توان دوم برسانید یا دو بار در خودش ضرب کنید. به عنوام مثال، مربع یا مجذور 10، عدد 100 می شود.
- جذر = رادیکال: به عنوان مثال، جذر عدد 36، عدد 6 می شود. برخی اعداد مانند 36 جذر کامل دارند و برخی اغداد مانند 8، جذر کامل و درستی ندارند.
- ریشۀ دوم: تفاوت ریشۀ دوم و رادیکال در این است که در ریشۀ دوم، عدد حاصل شده هم با علامت مثبت و هم با علامت منفی بیان می شود. مثلاً ریشۀ دوم عدد 36، عدد 6+ و عدد 6- می شود در صورتی که جذر یا رادیکال 36، عدد 6 فقط می شود.
- مکعب: مکعیب عدد x یعنی x3. به عبارت دیگر آن عبارت را به توان 3 برسانید یا سه بار در خودش ضرب کنید. به عنوان مثال مکعب 5، عدد 125 می شود.
- کعب = رادیکال فرجۀ سه = ریشۀ سوم: همۀ اینها یک مفهوم دارند. به عنوان مثال کعب عدد 8، عدد 2 می شود. برخی اعداد مانند 8، ریشۀ سوم کامل دارند و برخی اعداد مانند ماندد 10، ریشۀ سوم کامل و درستی ندارند.
- جملات متشابه: جملاتی که حرف انگلیسی و توان آنها مانند هم است مانند 5x2 و 8x2. جملات متشابه با هم قابلیت جمع و تفریق دارند مثلاً 8x2+5x2=13x2 می شود. جملات غیز متشابه، نمی توانند با هم جمع شوند. به عنوان مثال دو جملۀ 5x2-8x را در نظر بگیرید. از این ساده تر دیگر نمی توان آنها را نوشت!
- مجموع مجذور: دو عدد x و y را در نظر بگیرید. مجموع مجذور یا مجموع مربع x و y را به صورت x2+y2 نمایش می دهند. (اول توان 2 بعداً جمع)
- مجذور مجموع: دو عدد x و y را در نظر بگیرید. مجذور مجموع یا مربع مجموع x و y را به صورت 2(x+y) نمایش می دهند. (اول جمع کن بعد حاصل را به توان 2 ببرد.)
- مجموع مکعب: دو عدد x و y را در نظر بگیرید. مجموع مکعب آنها به صورت x3+y3 است. (اول به توان 3 ببر و بعد حاصل ها را با هم جمع کن.)
- مکعب مجموع: دو عدد x و y را در نظر بگیرید. مکعب مجموع آنها به صورت 3(x+y) است. (اول جمع کن و بعد حاصل را به توان 3 ببرید.)
مقالات مرتبط:
دانلود نمونه سوالات امتحانی ریاضی هفتم
