استادلینک، جامع ترین سایت جستجوی استاد خصوصی در سراسر کشور می باشد که با مراجعه به صفحه اصلی سایت استادلینک می توانید لیست بهترین اساتید دانشگاهی را به همراه رزومه، فیلم نمونه تدریس، نظر شاگردان قبلی، اطلاعات تماس مدرس و … مشاهده کرده و در صورت لزوم با آنها مستقیم ارتباط بگیرید.
همچنین می توانید برای مشورت در زمینۀ رزرو بهترین استاد خصوصی با توجه به شرایطتان و مشورت در مورد کنکور کارشناسی ارشد و کنکور دکتری، از طریق پشتیبانی سایت استادلینک اقدام نمایید.
آنچه در این مقاله می‌خوانید
بهترین استاد ریاضیات و الکترومغناطیس اصفهان
برای رزرو کلاس های خصوصی آنلاین و حضوری ریاضیات و الکترومغناطیس مهندس امید نجفی پور می توانید با شماره 09130394201 آکادمی نجفی تماس حاصل نمایید.
مرکز مشاوره درسی تحصیلی آکادمی نجفی
گروه آموزشی و مشاوره و برنامه ریزی تحصیلی و درسی
شماره تماس : 09130394201
نظرات دانش آموزان
آدرس: فلکه احمدآباد – خیابان جی – نرسیده به چهارراه پروین – کوچه ظفر (21)
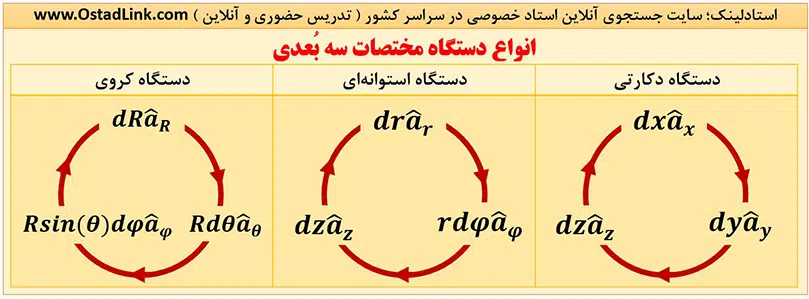
آشنایی با انواع دستگاه های مختصات
در تصویر زیر با سه دشتگاه معروف مختصات یعتی دستگاه دکارتی، دستگاه مختصات استوانه ای و دستگاه مختصات کروی آشنا می شوید.
تعریف نماد دل ∇ در ریاضی
نماد ∇ را در ریاضی نماد دل – Del ( برعکس علامت دلتا Δ ) می شناسند و به آن نابلا ( Nabla ) نیز می گویند. در مختصات دلخواه تعریف نماد دل به صورت زیر است.
توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.
![\[\overrightarrow{\mathrm{\nabla }}=\frac{\partial }{h_1.\partial u_1}{\hat{a}}_{u_1}+\frac{\partial }{h_2.\partial u_2}{\hat{a}}_{u_2}+\frac{\partial }{h_3.\partial u_3}{\hat{a}}_{u_3}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-c037e22cb981e122e0000c772e2d2f9d_l3.png "Rendered by QuickLaTeX.com")
اپراتور دل در دستگاه مختصات دکارتی
نماد دل در مختصات دکارتی به صورت زیر تعریف می شود.
![\[\overrightarrow{\mathrm{\nabla }}=\frac{\partial }{\partial x}{\hat{a}}_x+\frac{\partial }{\partial y}{\hat{a}}_y+\frac{\partial }{\partial z}{\hat{a}}_z\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-889f7c294fcd1319f7d95c624d19e9c8_l3.png "Rendered by QuickLaTeX.com")
اپراتور دل در دستگاه مختصات استوانه ای
نماد دل در مختصات استوانه ای به صورت زیر تعریف می شود.
![\[\overrightarrow{\mathrm{\nabla }}=\frac{\partial }{\partial r}{\hat{a}}_r+\frac{\partial }{r.\partial \varphi }{\hat{a}}_{\varphi }+\frac{\partial }{\partial z}{\hat{a}}_z\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-28451a8100c8812a9932b2c3909f9c2c_l3.png "Rendered by QuickLaTeX.com")
اپراتور دل در دستگاه مختصات کروی
نماد دل در مختصات دکارتی به صورت زیر تعریف می شود.
![\[\overrightarrow{\mathrm{\nabla }}=\frac{\partial }{\partial R}{\hat{a}}_R+\frac{\partial }{R.\partial \theta }{\hat{a}}_{\theta }+\frac{\partial }{Rsin(\theta ).\partial \varphi }{\hat{a}}_{\varphi }\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-089dcc4fb617202e936870773aa945bd_l3.png "Rendered by QuickLaTeX.com")
معادله لاپلاسین (Laplacian) در ریاضیات
معادله لاپلاس، یک تابع اسکالر را به یک تابع اسکالر دیگر تبدیل می کند و کاربرد زیادی در مهندسی دارد. در ادامه به تعریف معادله لاپلاس و فرمول آن در مختصات کلی، مختصات دکارتی، مختصات استوانه ای و مختصات کروی می پردازیم.
تعریف معادله لاپلاس ( لاپلاسین ) در ریاضی و الکترومغناطیس
به دیورژانس گرادیان یک تابع اسکالر مانند f، معادله لاپلاس ( لاپلاسین ) آن تابع اسکالر می گویند و با نماد 2f∇ نمایش می دهند که خود نیز یک تابع اسکالر است.
![\[{\nabla }^2f=\frac{1}{h_1h_2h_3}\left[\frac{\partial }{\partial u_1}\left(\frac{h_2h_3}{h_1}.\frac{\partial f}{\partial u_1}\right)+\frac{\partial }{\partial u_2}\left(\frac{h_1h_3}{h_2}.\frac{\partial f}{\partial u_2}\right)+\frac{\partial }{\partial u_3}\left(\frac{h_1h_2}{h_3}.\frac{\partial f}{\partial u_3}\right)\right]\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-1b8dfd3b365266c02b374d8e637c537a_l3.png "Rendered by QuickLaTeX.com")
برخی کاربرهای معادله لاپلاس در علوم مهندسی
- معادله ولتاژ الکترواستاتیک: می دانیم بار الکتریکی آزاد در رساناها وجود ندارد پس 2v=0∇ است.
- معادلۀ موج دو بعدی: معادلۀ موج دوبعدی به صورت روبرو تعریف می شود: utt=c2∇2u
- معادلۀ گرمای دو بعدی: معادلۀ گرمای دوبعدی به صورت روبرو تعریف می شود: ut=c2∇2u
“The Laplacian occurs in many differential equations describing physical phenomena. Poisson’s equation describes electric and gravitational potentials; the diffusion equation describes heat and fluid flow; the wave equation describes wave propagation; and the Schrödinger equation describes the wave function in quantum mechanics. In image processing and computer vision, the Laplacian operator has been used for various tasks, such as blob and edge detection. The Laplacian is the simplest elliptic operator and is at the core of Hodge theory as well as the results of de Rham cohomology.”
ترجمه‌ی دقیق فارسی:
«لاپلاسین در بسیاری از معادلات دیفرانسیلی که پدیده‌های فیزیکی را توصیف می‌کنند ظاهر می‌شود. معادله‌ی پواسون پتانسیل‌های الکتریکی و گرانشی را توصیف می‌کند؛ معادله‌ی پخش (انتشار) جریان گرما و سیال را توصیف می‌کند؛ معادله‌ی موج انتشار موج را توصیف می‌کند؛ و معادله‌ی شرودینگر تابع موج را در مکانیک کوانتومی توصیف می‌کند. در پردازش تصویر و بینایی کامپیوتری، عملگر لاپلاسین برای انجام کارهای مختلفی مانند آشکارسازی لکه‌ها (blob detection) و لبه‌ها استفاده شده است. لاپلاسین ساده‌ترین عملگر بیضوی است و در مرکز نظریه‌ی هاج و همچنین نتایج هم‌همولوژی دو رَهم قرار دارد.»
لینک دقیق منبع: ویکی پدیا
تماس
تلگرام
واتساپ
ایتافرمول لاپلاسین در دستگاه مختصات دکارتی
دز مختصات دکارتی با سه کمیت (x,y,z) سروکار داریم و ضرائب متری (Metric Coefficient) در آن (h1=h2=h3=1) همگی یک هستند. معادله لاپلاس در مختصات دکارتی به صورت زیر تعریف می شود.
![\[{\nabla }^2f=\frac{{\partial }^2f}{\partial x^2}\mathrm{+} \frac{{\partial }^2f}{\partial y^2} +\frac{{\partial }^2f}{\partial z^2}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-d2506df0e78c940dcf526deac0fc5744_l3.png "Rendered by QuickLaTeX.com")
فرمول لاپلاسین در دستگاه مختصات استوانه ای
در مختصات استوانه ای با سه کمیت (r,φ,z) سروکار داریم و ضرائب متری (Metric Coefficient) در آن به صورت (h1=1 , h2=r , h3=1) است. معادله لاپلاس در مختصات استوانه ای به صورت زیر تعریف می شود.
![\[{\nabla }^2f=\frac{1}{r}.\frac{\partial }{\partial r}\left(r.\frac{\partial f}{\partial r}\right)\mathrm{+}\frac{\mathrm{1}}{r^2}. \frac{{\partial }^2f}{\partial {\varphi }^2} +\frac{{\partial }^2f}{\partial z^2}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-2670f158daa2cedfd2206ea5a0b12819_l3.png "Rendered by QuickLaTeX.com")
فرمول لاپلاسین در دستگاه مختصات کروی
در مختصات کروی با سه کمیت (R,θ,φ) سروکار داریم و ضرائب متری (Metric Coefficient) در آن به صورت (h1=1 , h2=R , h3=Rsinθ) است. معادله لاپلاس در مختصات کروی به صورت زیر تعریف می شود.
![\[{\nabla }^2f=\frac{1}{R^2}.\frac{\partial }{\partial R}\left(R^2.\frac{\partial f}{\partial R}\right)\mathrm{+}\frac{\mathrm{1}}{R^2sin\left(\theta \right)}.\frac{\partial }{\partial \theta }\left(sin\left(\theta \right).\frac{\partial f}{\partial \theta }\right)+\frac{\mathrm{1}}{R^2sin^2\left(\theta \right)}.\frac{{\partial }^2f}{\partial {\varphi }^2}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-764f67dcaf15e3576fb1e4bf689dfd32_l3.png "Rendered by QuickLaTeX.com")
معادله پواسون و لاپلاس در الکترومغناطیس
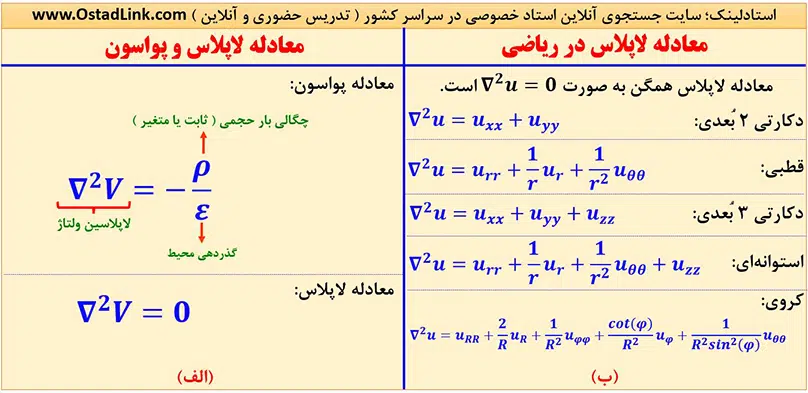
معادله پواسون و لاپلاس در سکل بالا قسمت (لف) بیان شده و همچنین معادله لاپلاس در ریاضیات مهندسی در تمامی دستگاه های مختصات 2 بعدی و 3 بعدی نیز در قسمت (ب) تصویر بالا آورده شده است.
مقالات مرتبط
آموزش دیورژانس به زبان ساده
آموزش معادله گردایان به زبان ساده
آموزش تبدیل لاپلاس به زبان ساده
آموزش تبدیل فوریه به زبان ساده
آموزش سری فوریه به زبان ساده