آموزش فرمول کرل (Curl) در ریاضی به زبان ساده

استادلینک، جامع ترین سایت جستجوی استاد خصوصی در سراسر کشور می باشد که با مراجعه به صفحه اصلی سایت استادلینک می توانید لیست بهترین اساتید دانشگاهی را به همراه رزومه، فیلم نمونه تدریس، نظر شاگردان قبلی، اطلاعات تماس مدرس و … مشاهده کرده و در صورت لزوم با آنها مستقیم ارتباط بگیرید.

همچنین می توانید برای مشورت در زمینۀ رزرو بهترین استاد خصوصی با توجه به شرایطتان و مشورت در مورد کنکور کارشناسی ارشد و کنکور دکتری، از طریق پشتیبانی سایت استادلینک اقدام نمایید.

آنچه در این مقاله می‌خوانید

بهترین استاد ریاضیات و الکترومغناطیس

برای رزرو کلاس های خصوصی آنلاین و حضوری ریاضیات و الکترومغناطیس مهندس امید نجفی پور می توانید با شماره 09130394201 آکادمی نجفی تماس حاصل نمایید.

مرکز مشاوره درسی تحصیلی آکادمی نجفی

گروه آموزشی و مشاوره و برنامه ریزی تحصیلی و درسی

شماره تماس : 09130394201

تماس

نظرات دانش آموزان

مشاهده نظرات

آدرس: فلکه احمدآباد – خیابان جی – نرسیده به چهارراه پروین – کوچه ظفر (21)

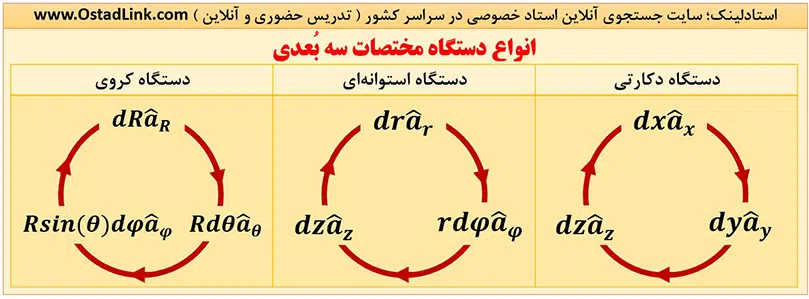
آشنایی با انواع دستگاه های مختصات

در تصویر زیر با سه دشتگاه معروف مختصات یعتی دستگاه دکارتی، دستگاه مختصات استوانه ای و دستگاه مختصات کروی آشنا می شوید.

تعریف نماد دل ∇ در ریاضی

نماد ∇ را در ریاضی نماد دل – Del ( برعکس علامت دلتا Δ ) می شناسند و به آن نابلا ( Nabla ) نیز می گویند. در مختصات دلخواه تعریف نماد دل به صورت زیر است.

توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.

$\overrightarrow{\mathrm{\nabla }}=\frac{\partial }{h_1.\partial u_1}{\hat{a}}_{u_1}+\frac{\partial }{h_2.\partial u_2}{\hat{a}}_{u_2}+\frac{\partial }{h_3.\partial u_3}{\hat{a}}_{u_3}$

اپراتور دل در دستگاه مختصات دکارتی

نماد دل در مختصات دکارتی به صورت زیر تعریف می شود.

$\overrightarrow{\mathrm{\nabla }}=\frac{\partial }{\partial x}{\hat{a}}_x+\frac{\partial }{\partial y}{\hat{a}}_y+\frac{\partial }{\partial z}{\hat{a}}_z$

اپراتور دل در دستگاه مختصات استوانه ای

نماد دل در مختصات استوانه ای به صورت زیر تعریف می شود.

$\overrightarrow{\mathrm{\nabla }}=\frac{\partial }{\partial r}{\hat{a}}_r+\frac{\partial }{r.\partial \varphi }{\hat{a}}_{\varphi }+\frac{\partial }{\partial z}{\hat{a}}_z$

اپراتور دل در دستگاه مختصات کروی

نماد دل در مختصات دکارتی به صورت زیر تعریف می شود.

$\overrightarrow{\mathrm{\nabla }}=\frac{\partial }{\partial R}{\hat{a}}_R+\frac{\partial }{R.\partial \theta }{\hat{a}}_{\theta }+\frac{\partial }{Rsin(\theta ).\partial \varphi }{\hat{a}}_{\varphi }$

کرل (Curl) در ریاضیات

کرل، یک تابع برداری را به یک تابع برداری دیگر تبدیل می کند و مفهومی شبیه چرخش و پیچش در یک سطح را دارد. در ادامه به تعریف کرل و فرمول آن در مختصات کلی، مختصات دکارتی، مختصات استوانه ای و مختصات کروی می پردازیم.

ارتباط با ما

از طریق راه های ارتباطی زیر می‌توانید با آکادمی نجفی در ارتباط باشید.

تعریف کرل در ریاضی

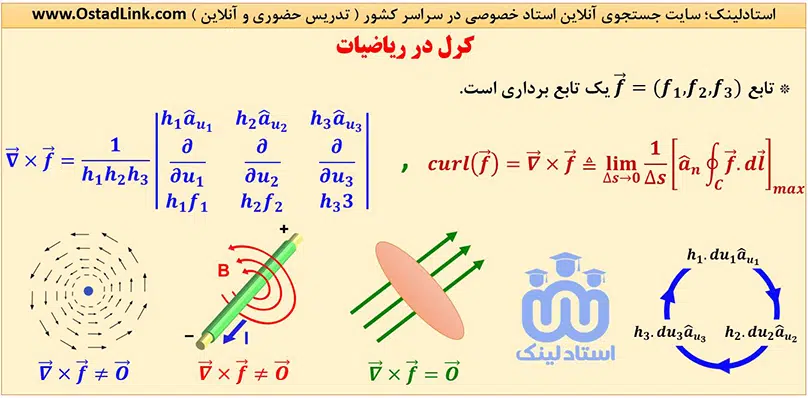
کرل، برداری است که اندازۀ آن حداکثر گردش خالص بردار f در واحد سطح است به طوری که سطح به سوی صفر میل می کند و جهت آن جهت عمودی سطح است زمانی که سطح طوری جهت داده شده باشد که گردش خالص را حداکثر نماید.

فرمول کرل در دستگاه مختصات دکارتی

تابع f=(f1,f2,f3) یک تابع برداری در مختصات دکارتی است. می دانیم ضرائب متری (Metric Coefficient) در مختصات دکارتی (h₁=h₂=h₃=1) همگی یک هستند. کرل در مختصات دکارتی به صورت زیر تعریف می شود.

فرمول کرل در دستگاه مختصات استوانه ای

تابع f=(f1,f2,f3) یک تابع برداری در مختصات استوانه ای است. می دانیم ضرائب متری (Metric Coefficient) در مختصات استوانه ای به صورت (h₁=1 , h₂=r , h₃=1) می باشد. کرل در مختصات استوانه ای به صورت زیر تعریف می شود.

فرمول کرل در دستگاه مختصات کروی

تابع f=(f1,f2,f3) یک تابع برداری در مختصات کروی است. می دانیم ضرائب متری (Metric Coefficient) در مختصات کروی به صورت
(h₁=1 , h₂=R , h₃=Rsinθ) است. کرل در مختصات کروی به صورت زیر تعریف می شود.

قضیه استوکس در ریاضی و الکترومغناطیس

در بخش پیشین کرل یک تابع برداری را به صورت انتگرال خظی مسیر بسته در واحد سطح بیان کردیم. اثبات می شود که انتگرال سطحی کرل یک میدان برداری، روی یک سطح باز برابر انتگرال خطی بستۀ بردار روی مسیری است که سطح را دربر می گیرد. یعنی:

$\mathop{\int\!\!\!\!\int}\nolimits^{\ }_{\ s\ }{\left(\overrightarrow{\nabla }\times \overrightarrow{f}\right).d\overrightarrow{s}=\oint^{\ }_{\ c\ }{\overrightarrow{f}}.d\overrightarrow{l}}$

دو اتحاد صفر در الکترومغناطیس

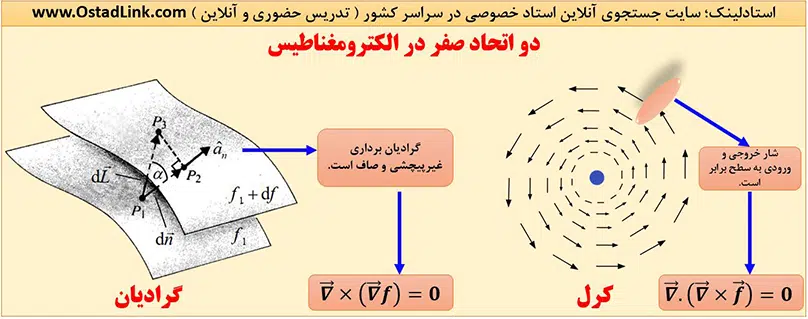
دو اتحاد عملیات مکرر del در مطالعۀ الکترومغناطیس اهمیت قابل ملاحظه ای دارند که به صورت زیر بیان می شوند:

اتحاد (1) صفر در الکترومغناطیس

کرل گرادیان هر میدان عددی، متحد با صفر است. یعنی:

$\overrightarrow{\mathrm{\nabla }}\times \left(\overrightarrow{\mathrm{\nabla }}f\right)=0$

اتحاد (2) صفر در الکترومغناطیس

دیورژانس کرل هر میدان برداری، متحد با صفر است. یعنی:

$\overrightarrow{\mathrm{\nabla }}.\left(\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{f}\right)=0$

“In electromagnetism, the curl of the electric field is proportional to the negative rate of change of the magnetic field, as expressed by Faraday’s law; the curl of the magnetic field is proportional to the current density and the rate of change of the electric field, as expressed by Ampère’s law with Maxwell’s correction.”

«در الکترومغناطیس، کرل میدان الکتریکی متناسب است با نرخ منفیِ تغییرات زمانیِ میدان مغناطیسی، طبق قانون فاراده؛ و کرل میدان مغناطیسی متناسب است با چگالی جریان و نرخ تغییرات میدان الکتریکی، طبق قانون آمپر با تصحیح مکسول.»

منبع: ویکی پدیا

مقالات مرتبط:

آموزش گرادیان به زبان ساده

آموزش دیورژانس به زبان ساده

آموزش معادله لاپلاسین در الکترومغناطیس

آموزش تبدیل لاپلاس به زبان ساده

آموزش تبدیل فوریه به زبان ساده

آموزش سری فوریه به زبان ساده