فیلم آموزش مثلثات سال یازدهم + حل تمرینات کتاب (قسمت 1)

کلاس یازدهم
مرداد 1401
مطالعه 3 دقیقه

فیلم آموزش مثلثات سال یازدهم + حل تمرینات کتاب (قسمت 1)

کلاس یازدهم
14 مرداد 1401
مطالعه 3 دقیقه

قسمت اول فیلم انیمیشنی آموزش مثلثات سال یازدهم به زبان ساده ویژه رشته ریاضی و تجربی به همراه حل تمامی سوالات کتاب درسی و نکات امتحانی و کنکوری مثلثات

این فیلم آموزشی توسط تیم اساتید ریاضی سایت تدریس خصوصی استادلینک تهیه شده و استفاده از آن با ذکر منبع (استادلینک) بلامانع می باشد.

سایت جستجوی معلم خصوصی استادلینک

استادلینک؛ جامع ترین وبسایت جستجوی معلم خصوصی و مشاور درسی در سراسر کشور بوده که با مراجعه به صفحه اول سایت استادلینک، می توانید لیست بهترین اساتید ریاضی کشور را به همراه رزومه، سابقه کار و تحصیل، نظر شاگردان قبلی و فیلم نمونه تدریس آنها مشاهده کرده و به صورت مستقیم و بدون واسطه با آنها ارتباط بگیرید.

همچنین می توانید از طریق پشتیبانی واتساپ سایت استادلینک، اقدام به رزرو معلم خصوصی خود سراسر کشور کنید و تدریسی عالی به صورت حضوری یا مجازی را تجربه نمایید.

دانلود تمامی فرمول های مثلثات دبیرستان و کنکور

دانلود جزوه کامل ( تایپی ) فرمول های مثلثات ویژۀ کنکور و امتحانات

فیلم آموزش مثلثات سال یازدهم ( قسمت اول )

برای رزرو معلم خصوصی ریاضی خود، از طریق پشتیبانی واتساپ سایت تدریس خصوصی استادلینک، اقدام نمایید.

در داخل این فیلم آموزشی، علاوه بر آموزش مثلثات سال یازدهم به زبان ساده و به صورت انیمیشنی، تمامی تمرین های کتاب درسی مبحث مثلثات سال یازدهم برای دو رشته ریاضی و تجربی، حل شده است.

سرفصل های مثلثات و دانلود نمونه سوالات امتحانی

مثلثات از جمله مباحث مهمی است که در هر سه سال دهم، یازدهم و دوازدهم در کتاب های درسی آمده است. مطالب آن تقریباً تکمیل کننده هم بوده و اگر قسمتی را متوجه نشوید، باعث اشکال در دیگر قسمت ها خواهد شد.

مبحث مثلثات در کنکور سراسری حداقل 3 سوال به صورت مستقیم برای هر دو رشته ریاضی و تجربی داشته و در درس فیزیک نیز بسیار بسیار پرکاربرد است.

مثلثات سال دهم

در کتاب ریاضی سال دهم، فصل دوم مربوط به این درس بوده و شما در این بخش با مفاهیم اولیه سینوس و کسینوس آشنا می شوید که در مقالۀ « فرمول های کنکوری مثلثات سال دهم به همراه فیلم آموزشی » می توانید به طور کامل مباحث سال دهم این بخش را مطالعه نمایید.

دانلود نمونه سوال امتحانی ریاضی 1 دهم تجربی و ریاضی

برای آشنایی با نمونه سوالات امتحانی دیماه و خردادماه درس ریاضی 1 رشته دهم تجربی و ریاضی، روی عبارت زیر ضربه بزنید

دانلود نمونه سوالات درس ریاضی 1 دهم ریاضی و تجربی

برای رزرو معلم خصوصی ریاضی خود، از طریق پشتیبانی واتساپ سایت تدریس خصوصی استادلینک، اقدام نمایید.

مثلثات سال یازدهم

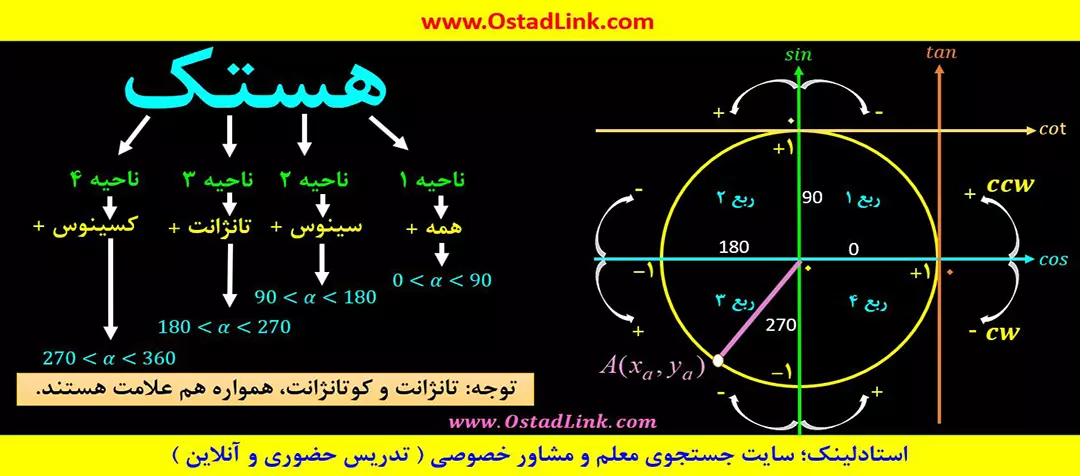
مباحث این درس در سال یازدهم به صورت زیر می باشد:

یادآوری دایره مثلثاتی
انواع واحدهای زاویه و یادآوری جدول زاویه های خاص
طول یک کمان – مساحت یک قطاع – رابطه بین دو قرقره متصل به هم
زاویه های ترکیبی
رابطه مجموع و تفاضل زاویه ها α±β
رابطه دو برابر کمان (2α)
توابع مثلثاتی و رسم نمودارهای سینوسی و کسینوسی

دانلود نمونه سوال امتحانی ریاضی 2 یازدهم تجربی و حسابان 1

برای آشنایی با نمونه سوالات امتحانی دیماه و خردادماه درس ریاضی 2 رشته یازدهم تجربی و درس حسابان 1 رشته یازدهم ریاضی فیزیک، روی عبارت های زیر ضربه بزنید.

برای رزرو معلم خصوصی ریاضی خود، از طریق پشتیبانی واتساپ سایت تدریس خصوصی استادلینک، اقدام نمایید.

مثلثات سال دوازدهم

سر فصل های این درس در سال دوازدهم به صورت زیر است:

تناوب و تانژانت
حل معادلات مثلثاتی

تقریباً می توان گفت در سال دوازدهم، هر آنچه که در سال دهم و یازدهم در مورد این مبحث مطالعه کرده اید نیاز بوده و پیشنهاد می کنیم بخاطر اهمیت این درس در کنکور، آنرا به صورت اصولی در کنار یک معلم خصوصی ریاضی با تجربه مطالعه نمایید.

دانلود سوال امتحان نهایی ریاضی 3 دوازدهم تجربی و حسابان 2

برای آشنایی با نحوۀ سوالات امتحان نهایی خرداد، شهریور و دیماه درس ریاضی 3 رشته دوازدهم تجربی و درس حسابان 2 رشته دوازدهم ریاضی فیزیک، به همراه پاسخ نامه تشریحی، روی عبارت های زیر ضربه بزنید.

برای رزرو معلم خصوصی ریاضی خود، از طریق پشتیبانی واتساپ سایت تدریس خصوصی استادلینک، اقدام نمایید.

نسبت های مثلثاتی زاویه های ترکیبی

توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.

فرمول های این بخش که در ویدئوی آموزش مثلثات سال یازدهم در قسمت بالا نیز مفصل و به صورت انیمیشنی گفته شد، به شرح زیر می باشد:

یادآوری: منظور از k عددی صحیح بوده و 2k نماد اعداد زوج و 2k-1 یا 2k+1 نماد اعداد فرد می باشد.

$k\in \mathbb{Z}$

$\mathbb{Z}=\{\dots ,-2,-1,0,1,2,\dots \}$

نسبت های مثلثاتی مضارب زوج 180 درجه

مضارب زوج 180 درجه، همان زاویۀ صفر هستند که در دو حالت جمع و تفریق بصورت مجزا بررسی می کنیم.

نسبت های مثلثاتی مضارب زوج 180 درجه در حالت جمع

در این حالت، انتهای کمان در ناحیه اول قرار دارد و همۀ نسبت ها علامت مثبت دارند.

${\mathrm{sin} \left(2k\pi +\alpha \right)\ }=+{\mathrm{sin} \left(\alpha \right)\ }$

${\mathrm{cos} \left(2k\pi +\alpha \right)\ }=+{\mathrm{cos} \left(\alpha \right)\ }$

${\mathrm{tan} \left(2k\pi +\alpha \right)\ }={\mathrm{+}\mathrm{tan} \left(\alpha \right)\ }$

${\mathrm{cot} \left(2k\pi +\alpha \right)\ }={\mathrm{+}\mathrm{cot} \left(\alpha \right)\ }$

نسبت های مثلثاتی مضارب زوج 180 درجه در حالت تفریق

در این حالت، انتهای کمان در ناحیه چهارم قرار دارد و فقط کسینوس علامت مثبت دارد.

${\mathrm{sin} \left(2k\pi -\alpha \right)\ }={\mathrm{-}\mathrm{sin} \left(\alpha \right)\ }$

${\mathrm{cos} \left(2k\pi -\alpha \right)\ }={\mathrm{+}\mathrm{cos} \left(\alpha \right)\ }$

${\mathrm{tan} \left(2k\pi -\alpha \right)\ }={\mathrm{-}\mathrm{tan} \left(\alpha \right)\ }$

${\mathrm{cot} \left(2k\pi -\alpha \right)\ }={\mathrm{-}\mathrm{cot} \left(\alpha \right)\ }$

نسبت های مثلثاتی مضارب فرد 180 درجه

مضارب زوج 180 درجه، همان زاویۀ 180 هستند که در دو حالت جمع و تفریق بصورت مجزا بررسی می کنیم.

نسبت های مثلثاتی مضارب فرد 180 درجه در حالت جمع

در این حالت، انتهای کمان در ناحیه سوم قرار دارد و فقط تانژانت و کتانژانت علامت مثبت دارند.

${\mathrm{sin} \left(\left(2k-1\right)\pi +\alpha \right)\ }=-{\mathrm{sin} \left(\alpha \right)\ }$

${\mathrm{cos} \left(\left(2k-1\right)\pi +\alpha \right)\ }=-{\mathrm{cos} \left(\alpha \right)\ }$

${\mathrm{tan} \left(\left(2k-1\right)\pi +\alpha \right)\ }=+{\mathrm{tan} \left(\alpha \right)\ }$

${\mathrm{cot} \left(\left(2k-1\right)\pi +\alpha \right)\ }=+{\mathrm{cot} \left(\alpha \right)\ }$

نسبت های مثلثاتی مضارب فرد 180 درجه در حالت تفریق

در این حالت، انتهای کمان در ناحیه دوم قرار دارد و فقط سینوس علامت مثبت دارند.

${\mathrm{sin} \left(\left(2k-1\right)\pi -\alpha \right)\ }=+{\mathrm{sin} \left(\alpha \right)\ }$

${\mathrm{cos} \left(\left(2k-1\right)\pi -\alpha \right)\ }=-{\mathrm{cos} \left(\alpha \right)\ }$

${\mathrm{tan} \left(\left(2k-1\right)\pi -\alpha \right)\ }=-{\mathrm{tan} \left(\alpha \right)\ }$

${\mathrm{cot} \left(\left(2k-1\right)\pi -\alpha \right)\ }=-{\mathrm{cot} \left(\alpha \right)\ }$

نسبت های مثلثاتی زاویه های قائمه در دایره مثلثاتی

زاویه های قائمه را می توان به دوستۀ 90 درجه و 180 درجه تقسیم بندی کرد. برای این منظور با فرض اینکه k عددی صحیح باشد، اعداد فرد را می توان به دو دسته تقسیم نمود:

اعداد فردی که با کم کردن یک واحد، بر عدد 4 بخشپذیر می شوند.
اعداد فردی که با اضافه کردن یک واحد بر عدد 4 بخشپذیر می شوند.

توجه: زاویه های قائمه، باعث تبدیل شدن نسبت ها به همزاد خود می شود.

1- اعداد فردی که با کم کردن یک واحد بر 4 بخشپذیر می شوند:

این اعداد را با نماد 4k+1 نمایش می دهند و داریم:

$4k+1=\left\{\dots ,-3,1,5,\dots \right\}$

2- اعداد فردی که با اضافه کردن یک واحد بر 4 بخشپذیر می شوند:

این اعداد را با نماد 4k-1 نمایش می دهند و داریم:

$4k-1=\left\{\dots ,-1,3,7,\dots \right\}$

نسبت های مثلثاتی زاویه های معادل 90 درجه

می توان این دسته از زاویه ها را در دو حالت جمع و تفریق بررسی نمود.

نسبت های مثلثاتی زاویه های معادل 90 درجه در حالت جمع

در این حالت، انتهای کمان در ناحیه دوم قرار دارد و فقط سینوس علامت مثبت دارد.

${\mathrm{sin} \left(\frac{\left(4k+1\right)\pi }{2}+\alpha \right)\ }=+{\mathrm{cos} \left(\alpha \right)\ }$

${\mathrm{cos} \left(\frac{\left(4k+1\right)\pi }{2}+\alpha \right)\ }=-{\mathrm{sin} \left(\alpha \right)\ }$

${\mathrm{tan} \left(\frac{\left(4k+1\right)\pi }{2}+\alpha \right)\ }=-{\mathrm{cot} \left(\alpha \right)\ }$

${\mathrm{cot} \left(\frac{\left(4k+1\right)\pi }{2}+\alpha \right)\ }=-{\mathrm{tan} \left(\alpha \right)\ }$

نسبت های مثلثاتی زاویه های معادل 90 درجه در حالت تفریق

در این حالت، انتهای کمان در ناحیه اول قرار دارد و همۀ نسبت ها علامت مثبت دارند.

${\mathrm{sin} \left(\frac{\left(4k+1\right)\pi }{2}-\alpha \right)\ }=+{\mathrm{cos} \left(\alpha \right)\ }$

${\mathrm{cos} \left(\frac{\left(4k+1\right)\pi }{2}-\alpha \right)\ }=+{\mathrm{sin} \left(\alpha \right)\ }$

${\mathrm{tan} \left(\frac{\left(4k+1\right)\pi }{2}-\alpha \right)\ }=+{\mathrm{cot} \left(\alpha \right)\ }$

${\mathrm{cot} \left(\frac{\left(4k+1\right)\pi }{2}-\alpha \right)\ }=+{\mathrm{tan} \left(\alpha \right)\ }$

نسبت های مثلثاتی زاویه های معادل 270 درجه

می توان این دسته از زاویه ها را در دو حالت جمع و تفریق بررسی نمود.

نسبت های مثلثاتی زاویه های معادل 270 درجه در حالت جمع

در این حالت، انتهای کمان در ناحیه چهارم قرار دارد و فقط کسینوس علامت مثبت دارد.

${\mathrm{sin} \left(\frac{\left(4k-1\right)\pi }{2}+\alpha \right)\ }=-{\mathrm{cos} \left(\alpha \right)\ }$

${\mathrm{cos} \left(\frac{\left(4k-1\right)\pi }{2}+\alpha \right)\ }=+{\mathrm{sin} \left(\alpha \right)\ }$

${\mathrm{tan} \left(\frac{\left(4k-1\right)\pi }{2}+\alpha \right)\ }=-{\mathrm{cot} \left(\alpha \right)\ }$

${\mathrm{cot} \left(\frac{\left(4k-1\right)\pi }{2}+\alpha \right)\ }=-{\mathrm{tan} \left(\alpha \right)\ }$

نسبت های مثلثاتی زاویه های معادل 270 درجه در حالت تفریق

در این حالت، انتهای کمان در ناحیه سوم قرار دارد و فقط تانژانت و کتانژانت علامت مثبت دارند.

${\mathrm{sin} \left(\frac{\left(4k-1\right)\pi }{2}-\alpha \right)\ }=-{\mathrm{cos} \left(\alpha \right)\ }$

${\mathrm{cos} \left(\frac{\left(4k-1\right)\pi }{2}-\alpha \right)\ }=-{\mathrm{sin} \left(\alpha \right)\ }$

${\mathrm{tan} \left(\frac{\left(4k-1\right)\pi }{2}-\alpha \right)\ }=+{\mathrm{cot} \left(\alpha \right)\ }$

${\mathrm{cot} \left(\frac{\left(4k-1\right)\pi }{2}-\alpha \right)\ }=+{\mathrm{tan} \left(\alpha \right)\ }$

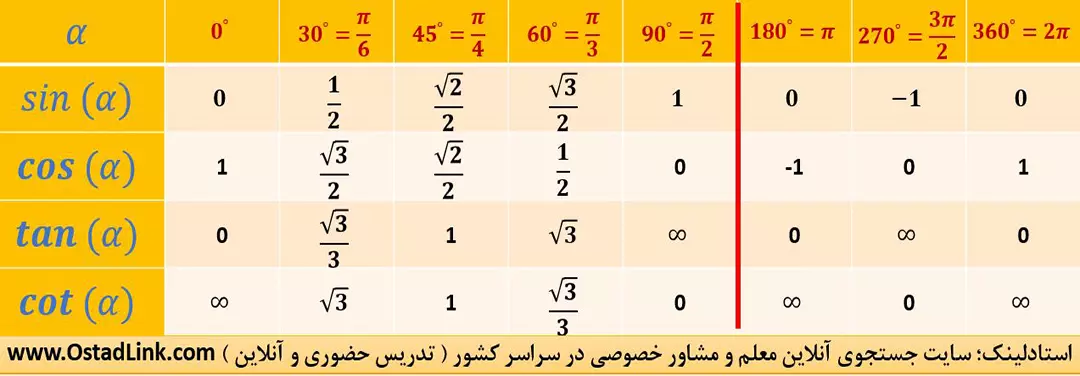
جدول زاویه ها در مثلثات

در جدول زیر، زاویه های مهمی که باید نسبت های مثلثاتی آنرا بدانید، آورده شده است.

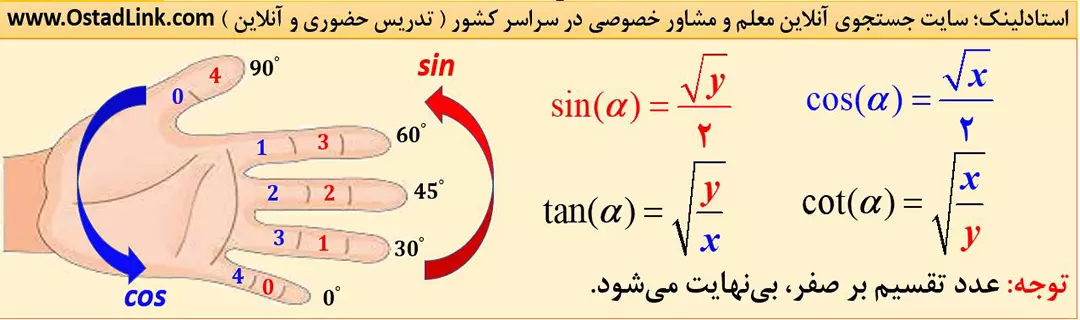
در عکس زیر، به کمک قاعدۀ دست چپ، میتوان نسبت های مثلثاتی زاویۀ صفر تا 90 درجه را به راحتی محاسبه کرد.

تمرین در خانه (H.W)

سوال: حاصل عبارت های زیر را بدست آورید و پاسخ نهایی خود را در بخش دیدگاه ها در پایین همین صفحه ثبت نمایید.

${\mathrm{sin} \left(-600\right)\ }$	${\mathrm{sin} \left(-\frac{10\pi }{3}\right)\ }$
${\mathrm{cos} \left(930\right)\ }$	${\mathrm{cos} \left(\frac{21\pi }{4}\right)\ }$
${\mathrm{tan} \left(-690\right)\ }$	${\mathrm{tan} \left(-\frac{19\pi }{6}\right)\ }$
${\mathrm{cot} \left(-210\right)\ }$	${\mathrm{cot} \left(\frac{31\pi }{6}\right)\ }$

دانلود تمامی فرمول های کنکوری مثلثات دبیرستان

در این بخش می توانید PDF فرمول های مثلثات ویژۀ کنکور و امتحانات را از سایت تدریس خصوصی استادلینک دانلود نمایید. برای دانلود جزوه کامل فرمول های مثلثات، کافی است روی عبارت زیر ضربه بزنید.

دانلود جزوه کامل ( تایپی ) فرمول های مثلثات ویژۀ کنکور و امتحانات

دعوت به همکاری در سایت تدریس خصوصی استادلینک

اگر شما علاقمند به تدریس خصوصی دروس مختلف از دبستان تا دانشگاه هستید، می توانید در سایت تدریس خصوصی استادلینک فعالیت نمایید. همچنین اگر توانایی تولید محتواهای درسی و علمی و مشاوره ای را دارید نیز می توانید با سایت معلم خصوصی استادلینک همکاری داشته باشید.

برای این منظور کافی است واژۀ «همکاری» را به پشتیبانی واتساپ سایت استادلینک ارسال نمایید و از توانایی های بالقوۀ خود درآمد بالا داشته باشید.

مقالات مرتبط :

فیلم آموزش قوانین و نحوه رسم تابع جز صحیح

فیلم آموزشی رسم توابع به کمک انتقال

فیلم آموزشی تجزیه عبارت های جبری

فیلم آموزشی و دانلود جزوه لگاریتم و توابع نمایی

قسمت دوم فیلم آموزش مثلثات سال یازدهم

داغ‌ترین مطالب روز

استاد حل نمونه سوالات امتحانی، تکالیف و پروژه های ماشین جریان متناوب AC

استاد حل تکالیف، تمرین ها، حل نمونه سوالات امتحانی آنلاین، سوالات کتاب درسی، حل سوالات جزوه، پروژه ها و شبیه سازی ماشین جریان متناوب AC در موسسه تکلاین (تکلیف آنلاین) استاد حل تکالیف ماشین جریان متناوب AC شاید برای شما پیش آمده باشد که وقت انجام تکالیف و نمونه سوالات امتحانی درس مورد نظر را […]

دانلود تمامی سوالات آزمون جامع سنجش تجربی نظام جدید

دانلود تمامی سوالات آزمون جامع سنجش رشته علوم تجربی نظام جدید از سال 1398 تا کنون به همراه جواب و پاسخنامه تشریحی توجه: استفاده از مطالب سایت جستجوی معلم خصوصی استادلینک با درج نام منبع ( سایت استادلینک ) بلامانع می باشد. دانلود سوالات آزمون جامع سنجش تجربی 1398 برای دانلود سوالات آزمون جامع سنجش […]

دانلود سوالات امتحان نهایی فیزیک تجربی دوازدهم شهریور 1401 + جواب

دانلود سوالات امتحان نهایی فیزیک دوازدهم تجربی شهریور ۱۴۰۱ همراه با پاسخنامه تشریحی + معرفی بهترین معلم خصوصی و تدریس خصوصی ویژه امتحانات نهایی رشته تجربی در ادامه با بارم بندی امتحان نهایی فیزیک 3 رشته تجربی و نحوه مطالعه صحیح این درس و راه حل پاس شدن در امتحانات نهایی و ترمیم معدل با […]