اتحادها، ابزاری برای محاسبات سریع تر در ریاضی هستند. در بخش قبل، آموزش اتحاد مربع دو جمله ای را مشاهده نمودید. در این آموزش، با فرمول اتحاد مکعب دو جمله ای همراه با مثال و فیلم آموزشی همراه ما باشید. این آموزش توسط سایت تدریس خصوصی استادلینک (همین سایت) برای شما عزیزان تهیه شده است.

فیلم آموزش ویدئویی اتحاد مکعب دو جمله ای

جهت رزرو معلم خصوصی ریاضی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

اصطلاحات رایج در ریاضی

در این بخش با مفاهیم و اصطلاحات رایج در ریاضی آشنا می شویم. حتماً قبل از آشنایی با اتحاد مکعب دو جمله ای، این مفاهیم را مرور کنید.

1. مربع = مجذور: مربع یا مجذور عدد x یعنی x². به عبارت دیگر یعنی آن عبارت را به توان دوم برسانید یا دو بار در خودش ضرب کنید.
2. جذر = رادیکال:  به عنوان مثال، جذر عدد 25، عدد 5 می شود. برخی اعداد مانند 25 جذر کامل دارند و برخی اعداد مانند 25 ، جذر کامل دارند و برخی اغداد مانند 10، جذر کامل ندارند.
3. ریشۀ دوم: تفاوت ریشۀ دوم و رادیکال در این است که در ریشۀ دوم، عدد حاصل شده هم با علامت مثبت و هم با علامت منفی بیان می شود. مثلاً ریشۀ دوم عدد 25، عدد 5+ و عدد 5- می شود در صورتی که جذر یا رادیکال 25، عدد 5 فقط می شود.
4. مکعب: مکعیب عدد x یعنی x³. به عبارت دیگر آن عبارت را به توان 3 برسانید یا سه بار در خودش ضرب کنید.
5. کعب = رادیکال فرجۀ سه – ریشۀ سوم: همۀ اینهایک مفهوم دارند. به عنوان نثال کعب عدد 8، عدد 2 می شود. برخی اعداد مانند 8، ریشۀ سوم کامل دارند و برخی اعداد مانند ماندد 10، ریشۀ سوم ندارند.
6. جملات متشابه: جملاتی که حرف انگلیسی و توان آنها مانند هم است مانند 5x² و 8x². جملات متشابه با هم قالیت جمع و تفریق دارند مثلاً 8x²+5x²=13x² می شود. جملات غیز متشابه، نمی توانند با هم جمع شوند. به عنوان مثال دو جملۀ 5x²-8x را در نظر بگیرید. از این ساده تر دیگر نمی توان آنها را نوشت!

توضیحات فرمول اتحاد مکعب دو جمله ای

اتحاد مکعب دو جمله ای، از دو عبارت غیرمتشابه داخل پرانتز که با هم جمع یا از هم کم شده اند و کل پردانتز به توان 3 رسیده است، تشکیل شده است. در شکل زیر، دو فرمول کلی اتحاد مکعب دو جمله ای را مشاهده می کنید.

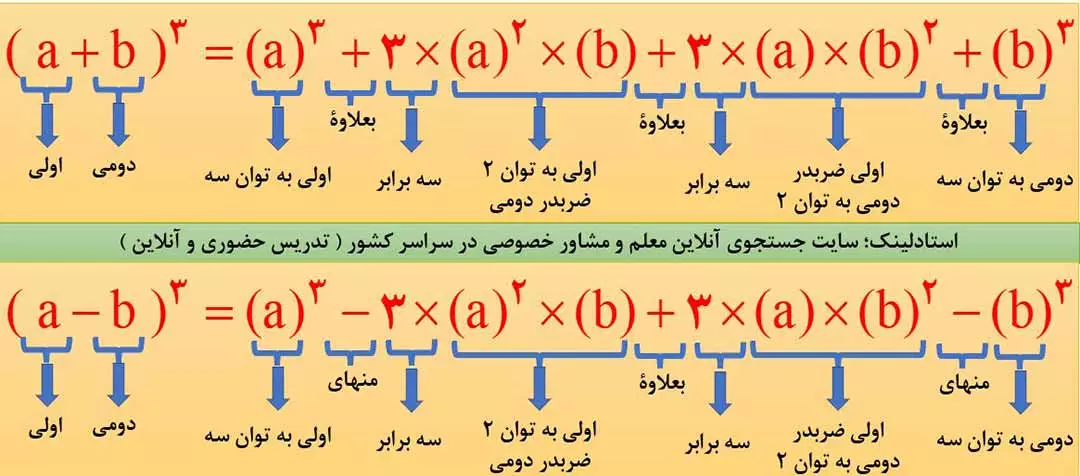
تکتۀ بسیار مهم: علامت عبارت اولی یعنی a را باید در فرمول لحاظ کنید ولی علامت عبارت دوم یعنی b را نباید ذز محاسبه لحاظ کنید. این مطلب را در فیلم آموزشی بالا به شما عزیزان آموزش خواهیم داد.

فرمول اتحاد مکعب سه جمله ای

فرمول زیر در کتاب های درسی و کتاب های کمک آموزشی وجود ندارد و صرفاً جهت استفادۀ علاقمندان ارائه شده است و در فیلم آموزشی بالا، توضیحات بیشتری در مورد آن ارائه شده است.

کاربرد اتحاد مکعب دو جمله ای

از اتحاد مکعب دو جمله ای، می توان به صورت محدود در تجزیۀ عبارت های جبری استفاده کرد. همچنین می توان برای محاسبۀ مکعب یک سری از اعداد (بدون حضور ماشین حساب) از این اتحاد کمک گرفت. در تصویر زیر، مثالی از کابرد اتحاد مکعب دو جمله ای را تماشا می کنید.

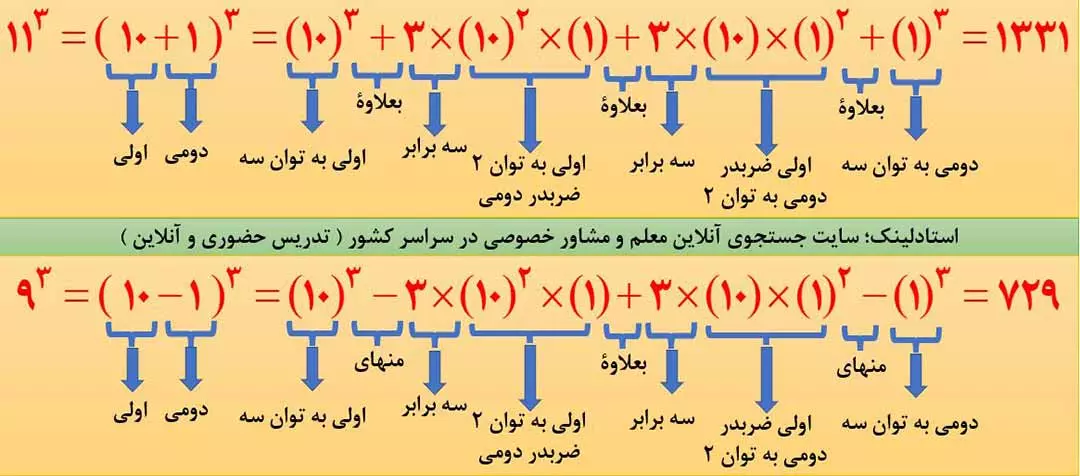
ترتیب عملیات ریاضی

در محاسبۀ اتحادها، هرگز ترتیب عملیات ریاضی را فراموش نکیند. ترتیب عملیات ریاضی به ترتیب الویت به صورت زیر است:

1. پرانتز یا کروشه
2. توان و جذر
3. ضرب و تقسیم
4. جمع و تفریق

توجه شود ترتیب گفته شده در بالا را رعایت کرده و دست آخر جمع و تفریق اعداد را از چپ به راست انجام دهید.

اگر در درس ریاضی متوسطۀ اول و دوم مشکل دارید، می توانید از اساتید خصوصی سایت استادلینک استفاده نمایید. استادلینک سایت جامع جستجوی معلم و مشاور خصوصی می باشد که با مراجعه صفحۀ اصلی سایت استادلینک، می توانید رزومه، سوابق، فیلم نمونه تدریس و نظر شاگردان قبلی استاد را مشاهده نموده و با معلم خصوصی خود به صورت مستقیم ارتباط بگیرید. همچنین می توانید از طریق پشتیبانی واتساپ سایت استادلینک، از ما نیز مشورت و مشاوره جهت گرفتن معلم خصوصی خود بگیرید.

تمرین در خانه: (Home Work)

اعداد 19³ و 21³ را به کمک اتحاد مکعب دو جمله ای حساب کنید و جواب خود را در بخش نظرات در پایین همین صفحه ارسال کنید.

مقالات مرتبط:

آموزش ویدئویی اتحاد مربع دو جمله ای همراه با مثال

فرمول اتحاد یک جمله مشترک همراه با مثال و فیلم آموزشی رایگان

دانلود سوالات هماهنگ استانی ریاضی نهم

چرا کلاس خصوصی استفاده کنیم؟