چگونه میتوانم دانلود بهترین جزوه فرمول های مشتق را انجام دهم؟

شما میتوانید در این مقاله از سایت استادلینک، کاملترین جزوه مشتق شامل تمامی فرمولهای دبیرستان و دانشگاه، تالیف مهندس امید نجفی را به صورت رایگان دانلود کنید.

بهترین استاد ریاضی دانشگاه در اصفهان برای تدریس خصوصی کیست؟

مهندس امید نجفی، مدرس برتر ریاضیات دانشگاهی در اصفهان، با سالها سابقه تدریس در آکادمی نجفی، آماده ارائه خدمات تدریس خصوصی ریاضیات مهندسی، معادلات و عمومی هستند. جهت هماهنگی با شماره 09130394201 تماس بگیرید.

آیا این مقاله تمامی فرمول های مشتق و کاربرد مشتق را پوشش میدهد؟

بله، در این آموزش جامع سعی شده است تمامی قوانین مشتقگیری، از مشتقات توابع جبری و مثلثاتی گرفته تا مشتقات جزئی و ضمنی به همراه کاربردهای آنها به زبانی ساده آموزش داده شود.

آدرس بهترین آموزشگاه ریاضی دانشگاه در اصفهان کجاست؟

آموزشگاه آکادمی نجفی واقع در اصفهان، خیابان جی، نرسیده به چهارراه پروین، ابتدای کوچه 21، به عنوان یکی از مراکز تخصصی آموزش ریاضیات دانشگاهی و کنکور فعالیت میکند.

آموزش تمامی فرمول های مشتق به زبان ساده

در این مقاله، با فرمول مشتق توابع چند جمله ای، مشتق توابع نمایی و لگاریتمی، مشتق توابع مثلثاتی و وارون مثلثاتی، مشتق توابع هیپربولیک و معکوس آن و مفهوم مشتق آشنا می شوید.

این مقاله توسط اساتید ریاضی سایت تدریس خصوصی استادلینک برای شما نوشته شده است. استادلینک، سامانۀ جتسجوی آنلاین استاد خصوصی ریاضی در سراسر کشور بوده که شما با مراجعه به صفحۀ اصلی سایت استادلینک می توانید رزومۀ برترین اساتید را مشاهده نمایید.

قرار داد: در این مباحث، a یک عدد حقیقی بوده و u و v توابع اسکالر یک متغیره می باشند.

آنچه در این مقاله می‌خوانید

بهترین استاد ریاضی دانشگاه در اصفهان

برای رزرو کلاس های خصوصی آنلاین و حضوری ریاضیات دانشگاهی مهندس امید نجفی پور می توانید با شماره 09130394201 آکادمی نجفی تماس حاصل نمایید.

مرکز مشاوره درسی تحصیلی آکادمی نجفی

گروه آموزشی و مشاوره و برنامه ریزی تحصیلی و درسی

شماره تماس : 09130394201

تماس

نظرات دانش آموزان

مشاهده نظرات

آدرس: فلکه احمدآباد – خیابان جی – نرسیده به چهارراه پروین – کوچه ظفر (21)

دانلود جزوه کامل فرمول های مشتق

برای دانلود جزوه کامل تمامی قواعد و جدول های مشتق گیری انواع توابع، روی جعبۀ زیر ضربه بزنید.

توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.

مشتق در توابع یک متغیره، شیب خط مماس بر تابع در نقطۀ مورد نظر را نشان می دهد که تعریف آن به زبان حد به صورت زیر است:

$\frac{\boldsymbol{df}}{\boldsymbol{dx}}\boldsymbol{=}{\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}\boldsymbol{=}{\mathop{\boldsymbol{lim}}_{\boldsymbol{\Delta }\boldsymbol{x}\boldsymbol{\to }\boldsymbol{0}} \frac{\boldsymbol{f}\left(\boldsymbol{x}\boldsymbol{+}\boldsymbol{\Delta }\boldsymbol{x}\right)\boldsymbol{-}\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}}{\boldsymbol{\Delta }\boldsymbol{x}}\ }$

قواعد مشتق گیری

برای ضرب، تقسیم، جمع، تفریق و ترکیب توابع از رابطه های زیر استفاده می نماییم.

${\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$u^{'\ }\pm v^{'\ }$	$u\pm v$
$u^{'~}.v+v^{'~}.u$	$u.v$
$\frac{u^{'~}.v-v^{'~}.u}{v^2}$	$\frac{u}{v}$
$\left(u^{'~}\right).f^{'~}(u)$	$f(u)$

توجه: می تواند ثابت کرد که ضریب و عدد در مخرج، اثری در مشتق گیری ندارند و باقی می مانند یعنی:

${\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$a.u^{'~}$	$a.u$
$\frac{u^{'~}}{a}$	$\frac{u}{a}$

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به موسسه آکادمی نجفی پیام دهید.

ارتباط با ما

از طریق راه های ارتباطی زیر می‌توانید با آکادمی نجفی در ارتباط باشید.

فرمول مشتق توابع چند جمله ای و رادیکالی

${\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$0$	$a$
$n.u^{n-1}.u^'$	$u^n$
$\frac{u^{'\ }}{2\sqrt{u}}$	$\sqrt{u}$
$\frac{u^'}{3\sqrt[2]{u^2}}$	$\sqrt[3]{u}$

فرمول مشتق توابع نمایی و لگاریتمی

توجه: a عددی حقیقی و u و v دو تابع هستند.

${\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$\left(u^'\right).e^u$	$e^u$
$\left(u^'\right).a^u.Ln(a)$	$a^u$
$u^v.[v^{'\ }.Ln\left(u\right)+\frac{u^{'\ }.v}{u}]$	$u^v$
$\frac{u'}{u}$	$Ln(u)$
$\frac{u^'}{u.Ln(a)}$	${{log}_a u\ }$

جهت رزرو معلم و استاد خصوصی ریاضی عمومی 1 و 2 به آموزشگاه آکادمی نجفی پیام دهید.

ارتباط با ما

از طریق راه های ارتباطی زیر می‌توانید با آکادمی نجفی در ارتباط باشید.

فرمول مشتق توابع مثلثاتی

${\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$\left(u^'\right).cos(u)$	$sin(u)$
$-\left(u^'\right).sin(u)$	$cos(u)$
$\left(u^'\right).sec^2(u)$	$tan(u)$
$-\left(u^'\right).csc^2(u)$	$cot(u)$
$\left(u^'\right).sec\left(u\right).tg(u)$	$sec(u)$
$-\left(u^'\right).~csc\left(u\right).cot(u)$	$csc(u)$

جهت رزرو استاد خصوصی معادلات دیفرانسیل به آموزشگاه ریاضی آکادمی نجفی پیام دهید.

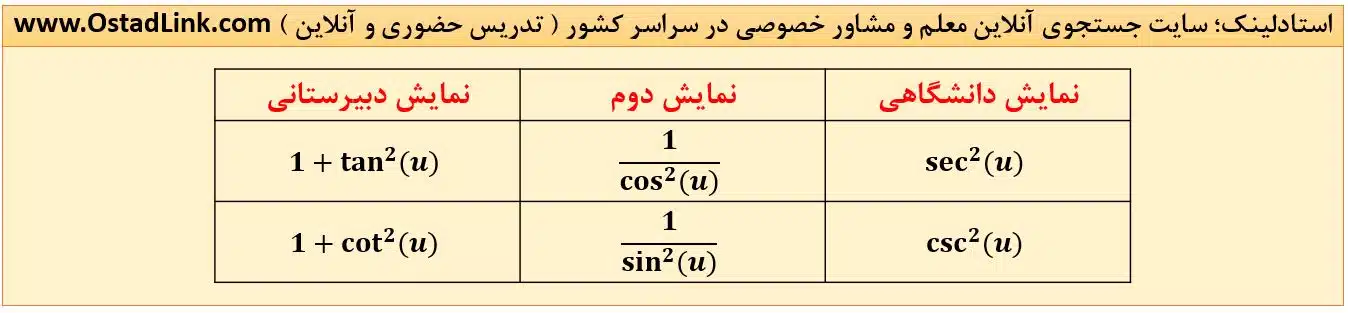
تعریف سکانت و کسکانت

سکانت و کسکانت به صورت زیر تعریف می شوند:

در شکل زیر با نمایش دیگر از دو تابع مثلثاتی آشنا می شوید:

فرمول مشتق توابع وارون مثلثاتی

${\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$\frac{u'}{\sqrt{1-u^2}}$	$sin^{-1}(u)$
$\frac{-(u^{'\ })}{\sqrt{1-u^2}}$	$cos^{-1}(u)$
$\frac{u'}{1+u^2}$	$tan^{-1}(u)$
$\frac{-\left(u^'\right)}{1+u^2}$	$cot^{-1}(u)$
$\frac{\pm 1}{u.\sqrt{u^2-1}}$	$s{ec}^{-1}(u)$
$\frac{\mp 1}{u.\sqrt{u^2-1}}$	${csc}^{-1}(u)$

توجه: محدودۀ توابع وارون مثلثاتی ( معکوس مثلثاتی ) باید در مشتق گیری رعایت شود که در مقاله ای دیگر به صورت مفصل به آن می پردازیم.

جهت رزرو استاد خصوصی ریاضی مهندسی به دپارتمان ریاضی آکادمی نجفی پیام دهید.

ارتباط با ما

از طریق راه های ارتباطی زیر می‌توانید با آکادمی نجفی در ارتباط باشید.

فرمول مشتق توابع هیپربولیک ( هذلولوی )

${\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$\left(u^'\right).cosh(u)$	$sinh(u)$
$\left(u^'\right).sinh(u)$	$cosh(u)$
$\left(u^'\right).se{ch}^2(u)$	$tanh(u)$
$-\left(u^'\right).cs{ch}^2(u)$	$coth(u)$
$-\left(u^'\right).sech\left(u\right).tgh(u)$	$sech(u)$
$-\left(u^'\right).csch\left(u\right).coth(u)$	$csch(u)$

توابع هیپربولیک ( هذلولی ) به صورت زیر تعریف می شوند:

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به آموزشگاه آکادمی مهندس امید نجفی پیام دهید.

فرمول مشتق توابع معکوس هیپربولیک

${\boldsymbol{f}}^{\boldsymbol{'\ }}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$\frac{u'}{\sqrt{u^2+1}}$	$sinh^{-1}(u)$
$\frac{\pm u'}{\sqrt{u^2-1}}$	$cosh^{-1}(u)$
$\frac{u'}{1-u^2}~,~\left\|u\right\|<1$	$tanh^{-1}(u)$
$\frac{u'}{1-u^2}~,~\left\|u\right\|>1$	$coth^{-1}(u)$
$\frac{\mp (u^{'\ })}{u.\sqrt{1-u^2}}$	$sech^{-1}(u)$
$\frac{-(u^{'\ })}{\|u\|.\sqrt{1+u^2}}$	$csch^{-1}(u)$

توجه: محدودۀ تعریف توابع وارون هیپربولیک جزء اهداف این مقاله نبوده و در مقالۀ دیگر به آن می پردازیم.

مشتق جزئی ( مشتق نسبی )

برای توابع چند متغیره از مشتق بستی استفاده می کنیم. فرض کنید f(x,y) یک تابع دو متغیره باشد، داریم:

$\frac{\partial f}{\partial x}=f_x={\mathop{lim}_{\Delta x\to 0} \frac{f\left(x+\Delta x,y\right)-f(x,y)}{\Delta x}\ }$

$\frac{\partial f}{\partial y}=f_y={\mathop{lim}_{\Delta y\to 0} \frac{f\left(x,y+\Delta y\right)-f(x,y)}{\Delta y}\ }$

مشتق جزئی - مشتق نسبی - دیفرانسیل توابع چند متغیره

دیفرانسیل توابع چند متغیره و مشتق مرتب بالاتر از توابع چند ضابطه ای، در تصویر بالا آمده است.

جهت کلاس خصوصی ریاضیات دانشگاهی به دپارتمان ریاضی مهندس نجفی پیام دهید.

ارتباط با ما

از طریق راه های ارتباطی زیر می‌توانید با آکادمی نجفی در ارتباط باشید.

گرادیان یک تابع اسکالر

گردایان یک تابع اسکالر به صورت زیر تعریف می شود:

گردایان در سه مختصات دکارتی استوانه ای و کروی

موارد زیر را خوب است در مورد گرادیان بدانید:

گرادیان، یک تابع اسکالر را به یک تابع برداری تبدیل می‏ کند.
گرادیان شبیه شیب خط در توابع تک متغیره است.
گرادیان یک میدان نرده‌ ای، میدانی برداری است که مؤلفه‌ های آن نرخ تغییر میدان نخستین را در جهت‌ های مختلف نشان می‌ دهد.
جهت خود میدان برداری گرادیان جهت بیشینۀ تغییرات است.

فرمول اندازه ( بزرگی ) یک بردار

اگر A(x,y,z) یک بردار در مختصات دکارتی باشد، اندازه یا بزرگی آن به صورت زیر تعریف می شود:

$\left|\overrightarrow{A}\right|=\sqrt{x^2+y^2+z^2}$

برای بدست آوردن بردار یکۀ هم راستا با بردار A یعنی e_A، از رابطۀ زیر استفاده می کنیم:

$e_A=\frac{\overrightarrow{A}}{|A|}$

مشتق سویی یا جهتی

برای تابع اسکالر f در نقطۀ p₀ در جهت بردار u، مشتق سویی یا جهتی به صورت زیر تعریف می شود:

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

مشتق زنجیره ای در توابع چند متغیره

قاعده زنجیره ای مشتق برای توابع چند متغیره به صورت زیر تعریف می شود که قابلیت تعمیم نیز دارد:

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

مشتق ضمنی

برای مشتق ضمنی تابع f(x,y,z)=0 به روش زیر می رویم:
( توجه کنید که حتما تابع f را باید مساوی صفر قرار دهیم و تمامی عبارت دز یک سمت تساوی باشد. )

$\frac{\partial z}{\partial x}=-\frac{f_x}{f_z}$

$\frac{\partial z}{\partial y}=-\frac{f_y}{f_z}$

$\frac{\partial y}{\partial x}=-\frac{f_x}{f_y}$

“The derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value).”

«مشتقِ یک تابع با متغیر حقیقی، میزان حساسیتِ تغییرات مقدار تابع (خروجی) را نسبت به تغییراتِ آرگومان (ورودی) آن اندازه‌گیری می‌کند.»

منبع: ویکی پدیا