سفارش تبلیغ در استادلینک

فرمول مشتق زنجیره ای همراه با نمونه سوالات و مثال مشتق زنجیره ای با جواب

در این مقاله مشتق زنجیره ای توابع به زبان ساده همراه با حل مثال و فیلم آموزشی رایگان و دانلود رایگان PDF فرمول های مشتق توسط اساتید استادلینک ارائه شده است.

فیلم آموزشی مشتق زنجیره ای

استادلینک، سایت جستجوی معلم و مشاور خصوصی در سراسر کشور بوده که شما می توانید لیست بهترین معلم های خصوصی را از صفحۀ اصلی سایت استادلینک مشاهده کرده و رزومه، سابقه تدریس، فیلم نمونه تدریس و نظر شاگردان قبلی اساتید را مشاهده نمایید.

همچنین می توانید جهت گرفتن معلم خصوصی ریاضی خود، به پشتیبانی واتساپ استادلینک، پیام دهید.

توجه: برای مشاهدۀ صحیح فرمول ها، در صورت استفاده از تلفن همراه، آنرا به صورت افقی قرار داده و موبایل خود را در حالت روشن ( light ) بگذارید.

مشتق چیست؟

به حاصل یکی از دو حد زیر، مشتق تابع f(x) در نقطۀ x=a می گویند.

$f^{'\ }\left(a\right)={\mathop{\mathrm{lim}}_{x\to a} \frac{f\left(x\right)-f(a)}{x-a}\ }$

$f^{'\ }\left(a\right)={\mathop{\mathrm{lim}}_{h\to 0} \frac{f\left(a+h\right)-f(a)}{h}\ }$

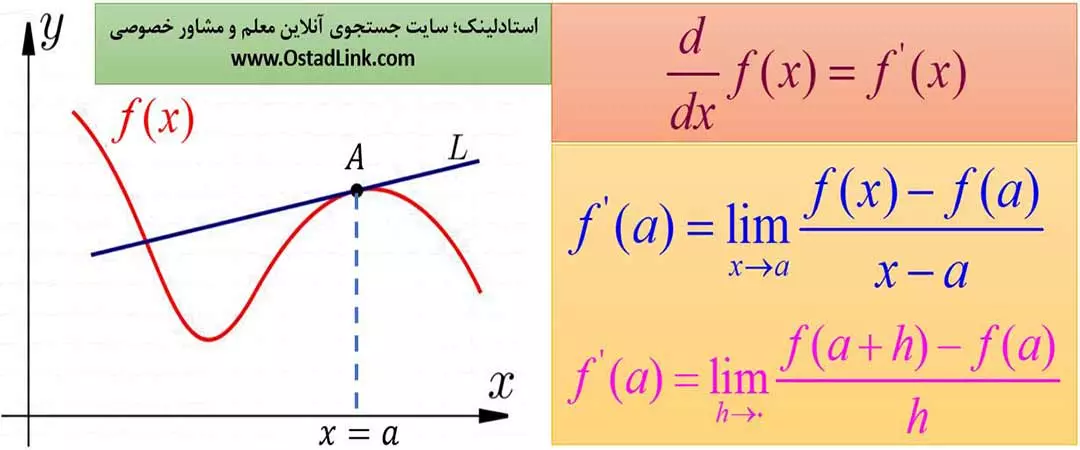
همانطور که مشاهده می کنید، مفهوم مشتق همان شیب خط مماس بر تابع f(x) در نقطۀ x=a است.

مشتق زنجیره ای مرتبه اول

دو تابع مشتق پذیر f(x) و g(x) را در نظر بگیرید. به fog(x) یا f(g(x))، ترکیب دو تابه f و g می گویند.

عبارت زیر ایدۀ اولیۀ استفاده از مشتق زنجیره ای مرتبه اول بوده که در ادامه روش ساده تر آن نیز بیان می شود.

$\frac{dy}{dx}=\frac{dy}{du}\times \frac{du}{dx}$

اگر توجه کنید، مشتق زنجیره ای، همان ترکیب دو تابع است. برای سادگی و بدون نیاز به رابطۀ بالا، می توان از رابطۀ زیر برای مشتق زنجیره ای مرتبه اول استفاده کرد.

${\left(fog(x)\right)}^{'\ }=g^{'\ }\left(x\right)\times f^{'\ }(g\left(x\right))$

در این قسمت برای سادگی در تلفظ می توان g(x) را به صورت u بیام کرد و f(g(x)) را به f(u) تغییر نام داد. بنابراین متشق زنجیره ای مرتبۀ اول به صورت زیر بیان می شود.

${\left(f\left(u\right)\right)}^{'\ }=u^{'\ }\times f^{'\ }(u)$

حل چند مثال از مشتق زنجیره ای توابع

$\mathrm{sin}\mathrm{}(x^{3\ }-5x+1){{\stackrel{'}{\rightarrow}(3x^{2\ }-5+0)\times \mathrm{cos}\mathrm{}(x^{3\ }-5x+1)}}$

$e^{{\mathrm{sin} \left(2x\right)\ }}{{\stackrel{'}{\rightarrow}}}2{\mathrm{cos} \left(2x\right)\ }.e^{\mathrm{sin}\mathrm{}(2x)}$

دانلود pdf تمامی فرمول های مشتق

برای دانلود PDF فرمول مستق دبیرستان و دانشگاه، اینجا ضربه بزنید. در این جزوه تمامی قواعد مشتق زنجیره ای آورده شده تا نیاز به اثبات آن نداشته باشید.

این جزوه توسط اساتید ریاضی سایت استادلینک تهیه شده و استفاده از آن با ذکر منبع بلامانع می باشد. این جزوه برای دبیرستان و دانشگاه مفید می باشد.

مشتق زنجیره ای مراتب بالاتر

این قسمت مربوط به دانشگاه می باشد و دانش آموزان دبیرستانی لازم به خواندن آن نیستند.

فرمول مشتق توابع جبری

$f^{'\:}\left(x\right)$	$f\left(x\right)$
$0$	$a$
$1$	$x$
$a$	$ax$
$a.u^'$	$au$
$a.n.u^{n-1}.\left(u\right)^'$	$a.u^n$
$\frac{\left(u\right)^'}{2\sqrt{u}}$	$\sqrt{u}$
$\frac{\left(u\right)^'}{3\sqrt[3]{\left(u\right)^2}}$	$\sqrt[3]{u}$
$\frac{n}{\:m}.u^{\frac{n}{m}-1}.\left(u\right)^'$	$\sqrt[m]{u^n}=u^{\frac{n}{m}}$

فرمول مشتق توابع مثلثاتی

$f^{'\:}\left(x\right)$	$f\left(x\right)$
$\left(u\right)^{'\:}.cos\left(u\right)$	$sin\left(u\right)$
$\left(u\right)^{'\:}.sin\left(2u\right)$	$sin^2\left(u\right)$
$n.sin^{n-1}\left(u\right).\left(u\right)^{'\:}.cos\left(u\right)$	$sin^n\left(u\right)$
$-\left(u\right)^{'\:}.sin\left(u\right)$	$cos\left(u\right)$
$-\left(u\right)^{'\:}.sin\left(2u\right)$	$cos^2\left(u\right)$
$-n.cos^{n-1}\left(u\right).\left(u\right)^{'\:}.sin\left(u\right)$	$cos^n\left(u\right)$
$\left(u\right)^{'\:}.\left(1+tan^2\left(u\right)\right)$	$tan\left(u\right)$
$n.tan^{n-1}\left(u\right).\left(u\right)^{'\:}.\left(1+tan^2\left(u\right)\right)$	$tan^{n\:}\left(u\right)$
$-\left(u\right)^{'\:}.\left(1+cot^2\left(u\right)\right)$	$cot\left(u\right)$
$-n.cot^{n-1}\left(u\right).\left(u\right)^{'\:}.\left(1+cot^2\left(u\right)\right)$	$cot^{n\:}\left(u\right)$

فرمول قواعد مشتق

$f^{'\:}\left(x\right)$	$f\left(x\right)$	نوع عملیات	شماره ردیف
$u^{'\:}+v^'$	$u+v$	جمع دو تابع	1
$u^{'\:}-v^'$	$u-v$	تفریق دو تابع	2
$u^{'\:}\cdot v+v^{'\:}\cdot u$	$u\cdot v$	ضرب دو تابع	3
$a\cdot u^'$	$a\cdot u$	ضرب عدد در یک تابع	4
$\frac{u^{'\:}\cdot v-v^{'\:}\cdot u}{v^2}$	$\frac{u}{v}$	تقسیم دو تابع	5
$\frac{u^'}{a}$	$\frac{u}{a}$	تقسیم تابع بر یک عدد	6
$\left(u\right)^{'\:}\cdot f^{'\:}\left(u\right)$	$f\left(u\right)$	ترکیب دو تابع با هم	7