در این فیلم آموزشی، به زبان ساده و به صورت کامل، مفهوم فازور و کاربرد فازور در مدارهای الکتریکی را برای بدست آوردن پاسخ حالت دائمی سینوسی آموزش داده شده است.
استادلینک؛ جامع ترین سایت انتخاب استاد خصوصی و مشاور درسی بوده که با مراجعه به صفحه اصلی سایت استادلینک می توانید لیست بهترین اساتید برق را به همراه فیلم نمونه تدریس و رزومه آنها مشاهده کرده و در صورت نیاز به صورت مستقیم با آنها ارتباط بگیرید.
فیلم آموزشی فازور در مدارهای الکتریکی
برای رزرو استاد خصوصی دروس دانشگاهی مورد نظر خود، به پشتیبانی واتساپ سایت استادلینک پیام دهید.
در این آموزش، پایه و اساس به دست آوردن جواب حالت دائمی سینوسی در مدارهای الکتریکی را به شما عزیزان به زبان ساده آموزش داده ایم.
فازور چیست؟
فازور نگاشتی است که شکل موج های سینوسی و کسینوسی با فرکانسهای یکسان را به حوزۀ اعداد مختلط، نگاشت میکند.
مزیت مهم نگاشت فازور چیست؟
مزیت مهم نگاشت فازور، تبدیل شدن معادلات دیفرانسیل به جمع و ضرب و تقسیم فازورها است یعنی از شرّ معادلۀ دیفرانسیل خلاص می شویم.
عیب و ایراد نگاشت فازور چیست؟
یکی از ایرادات و سختی این نگاشت، کار با اعداد مختلط است که برای برخی از افراد دلچسب و خوشایند نیست.
چند نگاشت معروف: تبدیل لاپلاس، تبدیل فوریه، لگاریتم و …
کابرد نگاشت های در ریاضی چیست؟
هدف همۀ نگاشت ها در ریاضی، ساده سازی محاسبات ریاضی است. همانطور که در تصویر بالا مشاهده می کنید، نگاشت لگاریتم یک علمیات پیچیدۀ ریاضی را به یک عملیات ساده تر طبق قوانینی تبدیل می کند یعنی:
- تبدیل توان به ضرب
- تبدیل ضرب به جمع
- تبدیل تقسیم به تفریق
یادآوری اعداد مختلط و چند رابطۀ ریاضی
توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.
الف) اعداد مختلط:
نماد اعداد مختلط به صورت زیر است:
![\[i=j=\sqrt{-1}\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-c6602293c88f590cdffca882e920bb46_l3.png "Rendered by QuickLaTeX.com")
نمایش دکارتی اعداد مختلط
نمایش دکارتی اعداد مختلط به صورت زیر است:
![\[z=x+jy\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-a1e68556937955956ccd886319eae0ea_l3.png "Rendered by QuickLaTeX.com")
که به x قسمت حقیقی یا Re(z) و به y قسمت موهومی یا Im(z) می گویند.
نمایش قطبی اعداد مختلط
نمایش قطبی اعداد مختلط به صورت زیر است:
![\[z=r\nprec \theta \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-0365cd8f36e31d2dc6e6e774ff6ec560_l3.png "Rendered by QuickLaTeX.com")
که به r اندازۀ عدد مختلط و به تتا، زاویۀ عدد مختلط می گویند.
تبدیل فرم دکارتی به فرم قطبی در اعداد مختلط
برای بدست آوردن اندازه از فرمول زیر استفاده می شود:
![\[r=\sqrt{x^2+y^2}\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-b77ce6c653a0b6daae66668bfe40b8e6_l3.png "Rendered by QuickLaTeX.com")
و برای بدست آوردن زاویه، داریم:
![\[\theta ={{\mathrm{tan}}^{-1} \left(\frac{y}{x}\right)\ }\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-e07094e4d1762f6f3c2be622db1ac635_l3.png "Rendered by QuickLaTeX.com")
تبدیل فرم قطبی به فرم دکارتی در اعداد مختلط
برای بدست آوردن قسمت حقیقی عدد مختلط از رابطۀ زیر استفاده می کنیم:
![\[x=r.{\mathrm{cos} \left(\theta \right)\ }\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-4395d1ca8153981df77800dc846bcc69_l3.png "Rendered by QuickLaTeX.com")
و برای بدست آوردن قسمت موهومی عدد مختلط به کمک فرم قطبی داریم:
![\[y=r.\mathrm{sin}\mathrm{}(\theta )\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-3bff4cfb278fde78b913c8b25b775705_l3.png "Rendered by QuickLaTeX.com")
توجه: برای جمع و تفریق اعداد مختلط بهتر است از فرم دکارتی و برای ضرب، تقسیم و توان رساندن اعداد مختلط بهتر است از فرم قطبی آن استفاده کنیم.
ب) بسط مک لورن چند تابع معروف
بسط مکلورن همان بسط تیلور در مبداء مختصات است.
بسط مک لورن تابع نمایی
![\[e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-53a99b87da6db80c72f8fe37fa6e2d69_l3.png "Rendered by QuickLaTeX.com")
بسط مک لورن تابع کسینوس
![\[{\mathrm{cos} \left(x\right)\ }=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\dots \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-2dcdea70d72973b844947b140dc08248_l3.png "Rendered by QuickLaTeX.com")
بسط مک لورن تابع سینوس
![\[{\mathrm{sin} \left(x\right)\ }=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\dots \]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-6993178def100543e6216379b9193322_l3.png "Rendered by QuickLaTeX.com")
پ) رابطۀ اویلر
آقای اویلر به کمک سه بسط بالا، مطابق آنچه در ویدئو گفته شد، به رابطۀ زیر رسید:
![\[e^{i\theta }={\mathrm{cos} \left(\theta \right)\ }+i.{\mathrm{sin} \left(\theta \right)\ }\]](https://ostadlink.com/blog/wp-content/ql-cache/quicklatex.com-2d6b66a64029d37dc5b3399944b69d11_l3.png "Rendered by QuickLaTeX.com")
پاسخ حالت دائمی سینوسی
می دانیم هر معادلۀ دیفرانسیل از دو جواب همگن و جواب خصوصی تشکیل شده است. در مدارهای پایدار، جواب همگن پس از 4 الی 5 ثابت زمانی به صفر میل می کند.
اگر ورودی مدار، توابع سینوسی هم فرکانس باشد، به جواب خصوصی یا حالت دائم آنها، پاسخ حالت دائمی سینوسی گفته می شود که همانطور که در فیلم گفته شد، می توان به کمک روابط فازور، آنها را به صورت ساده تری حل کرد.
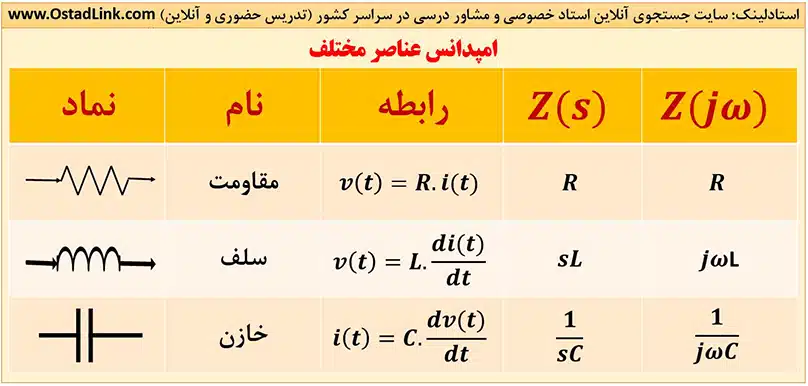
امپدانس چیست؟
به نسبت ولتاژ به جریان در حوزۀ لاپلاس زمانی که حالت اولیه المان صفر باشد، امپدانس یا مقاومت ظاهری می گویند. اگر بجای s از jw استفاده شود، امپدانس در حوزۀ فازور بدست می آید.
2 پاسخ
عالی
ممنونم خانم مهندس