دانلود جزوه کامل انتگرال | آموزش تمامی فرمول های انتگرال گیری

آموزش دروس دانشگاهی
در مهر 1402
مطالعه 3 دقیقه

دانلود جزوه کامل انتگرال | آموزش تمامی فرمول های انتگرال گیری

در این مقاله با فرمول های عمومی انتگرال گیری تمامی توابع مهم آشنا خواهید شد. دانلود کامل ترین جزوه جدول های انتگرال گیری از سایت استادلینک

استادلینک سایت جسنجوی معلم، استاد و مشاور خصوصی بوده که با مراجعه به صفحه اصلی سایت استادلینک، می توانید لیست بهترین اساتید را مشاهده کرده و با مشاهده ززومه و فیلم نمونه تدریس، استاد مورد نظر خود را برای تدریس خصوصی انتخاب نمایید.

دانلود جزوه کامل قواعد انتگرال گیری

دانلود جزوه کامل انتگرال و تمامی جدول ها و فرمول های انتگرال گیری

انتگرال، یک عملیات ریاضی ضد مشتق است که متاسفانه قاعدۀ خاصی برای انجام آن، وجود ندارد. روش های انتگرال گیری مختلفی وجود دارد که در این مقاله با جدول های انتگرال پر کابرد آشنا می شویم و سپس در مقالات دیگر روش های گوناگون انتگرال گیری را می آموزید.

قرارداد: در این مقاله a و b و p و q و n اعداد حقیقی و u و v تابع هستند.

توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.

$\boldsymbol{F}\left(\boldsymbol{x}\right)\boldsymbol{=}\int{\boldsymbol{f}\left(\boldsymbol{x}\right)\boldsymbol{dx}}$	$\boldsymbol{f}\boldsymbol{(}\boldsymbol{x}\boldsymbol{)}$
$a.\int{udx}$	$\int{a.udx}$
$\int{udx\pm \int{vdx}}$	$\int{\left(u\pm v\right)dx}$
$a.\int{udx\pm b.\int{vdx}}$	$\int{\left(a.u\pm b.v\right)dx}$

توجه: انتگرال خاصیت خطی بودن دارد.

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

فرمول انتگرال تابع چند جمله ای

$\int{\boldsymbol{f}\left(\boldsymbol{x}\right)\boldsymbol{dx}}$	$\boldsymbol{f}\left(\boldsymbol{x}\right)$
$a.x$	$a$
$\frac{x^{n+1}}{n+1}$	$x^n$
$\frac{{\left(ax+b\right)}^{n+1}}{a.(n+1)}$	${\left(ax+b\right)}^n$
$\frac{{2.\left(ax+b\right)}^{\frac{3}{2}}}{3a}$	$\sqrt{ax+b}$
$\frac{2\sqrt{ax+b}}{a}$	$\frac{1}{\sqrt{ax+b}}$

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

فرمول انتگرال تابع نمایی

$\int{\boldsymbol{f}\left(\boldsymbol{x}\right)\boldsymbol{dx}}$	$\boldsymbol{f}\left(\boldsymbol{x}\right)$
$\frac{e^{ax}}{a}$	$e^{ax}$
$\frac{b^{ax}}{a.Ln(b)}$	$b^{ax}$

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

فرمول انتگرال تابع مثلثاتی

$\int{\boldsymbol{f}\left(\boldsymbol{x}\right)\boldsymbol{dx}}$	$\boldsymbol{f}\left(\boldsymbol{x}\right)$
$\frac{cos(ax)}{-a}$	$sin(ax)$
$\frac{sin(ax)}{a}$	$cos(ax)$
$-\frac{1}{a}.Ln\|cos\left(ax\right)\|$	$tan(ax)$
$\frac{1}{a}.Ln\|sin\left(ax\right)\|$	$cot(ax)$
$\frac{1}{a}Ln\left(sec\left(ax\right)+tg\left(ax\right)\right)$	$sec(ax)$
$\frac{1}{a}Ln\left(csc\left(ax\right)-cot\left(ax\right)\right)$	$csc(ax)$
$\frac{1}{a}.tan(ax)$	$sec^2(ax)$
$\frac{-1}{a}.cot(ax)$	$csc^2(ax)$
$\frac{1}{a}.[tan\left(ax\right)-ax]$	$tan^2~(ax)$
$\frac{-1}{a}.[cot\left(ax\right)+ax]$	$cot^2(ax)$
$\frac{1}{2a}.[ax-\frac{1}{2}sin\left(2ax\right)]$	$sin^2(ax)$
$\frac{1}{2a}.[ax+\frac{1}{2}sin\left(2ax\right)]$	$cos^2(ax)$
$\frac{1}{a}.sec(ax)$	$sec\left(ax\right).tan(ax)$
$\frac{-1}{a}.csc(ax)$	$csc\left(ax\right).cot(ax)$

تعریف سکانت و کسکانت

سکانت و کسکانت یک تابع مثلثاتی هستند که به صورت زیر تعریف می شوند:

به عکس زیر دقت نمایید و نحوه نمایش دو فرمول مهم مثلثاتی را به خاطر بسپارید:

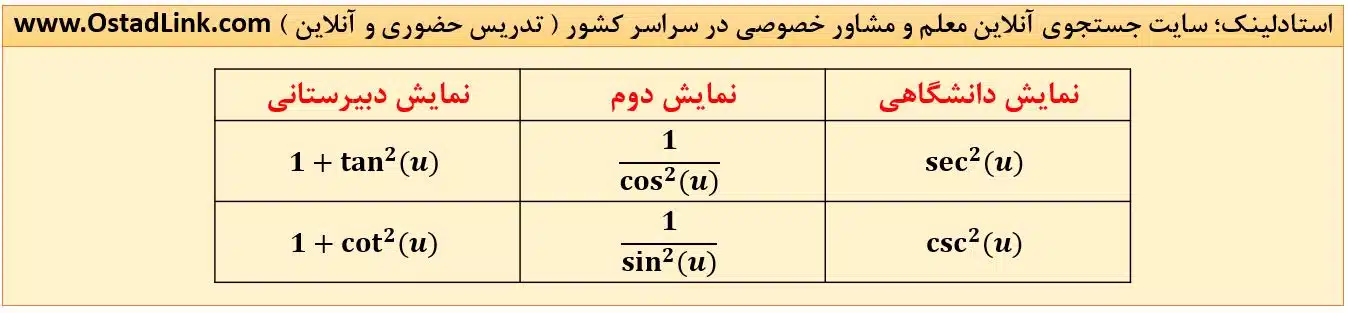
چند رابطه مهم مثلثاتی

1- تبدیل ضرب به جمع در مثلثات

2- رابطه های مهم مثلثاتی

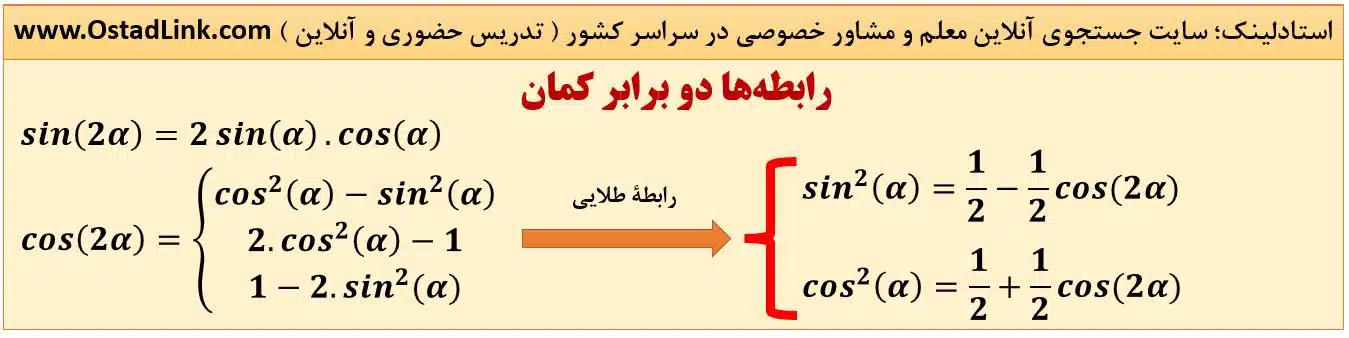
دو رابطۀ ذیگر مثلثاتی نیز وجود دارد که ممکن است در پاره ای از مواقع با آنها روبرو شوید:

فرمول انتگرال تابع معکوس مثلثاتی

$\int{\boldsymbol{f}\left(\boldsymbol{x}\right)\boldsymbol{dx}}$	$\boldsymbol{f}\left(\boldsymbol{x}\right)$
$x.sin^{-1}\left(\frac{x}{a}\right)+\sqrt{a^2-x^2}$	$sin^{-1}\left(\frac{x}{a}\right)$
$x.~{cos}^{-1}\left(\frac{x}{a}\right)-\sqrt{a^2-x^2}$	${cos}^{-1}\left(\frac{x}{a}\right)$
$x.~{tan}^{-1}\left(\frac{x}{a}\right)-\frac{a}{2}.Ln\left(x^2+a^2\right)$	$tan^{-1}\left(\frac{x}{a}\right)$
$x.~{cot}^{-1}\left(\frac{x}{a}\right)+\frac{a}{2}.Ln\left(x^2+a^2\right)$	${cot}^{-1}\left(\frac{x}{a}\right)$
$x.sec^{-1}\left(\frac{x}{a}\right)\mp a.Ln\left(x+\sqrt{x^2-a^2}\right)$	${sec}^{-1}\left(\frac{x}{a}\right)$
$x.csc^{-1}\left(\frac{x}{a}\right)\pm a.Ln\left(x+\sqrt{x^2-a^2}\right)$	${csc}^{-1}\left(\frac{x}{a}\right)$

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

فرمول انتگرال تابع هیپربولیک

$\int{\boldsymbol{f}\left(\boldsymbol{x}\right)\boldsymbol{dx}}$	$\boldsymbol{f}\left(\boldsymbol{x}\right)$
$\frac{1}{a}.\mathrm{cos}{\mathrm{h} \left(ax\right)\ }$	$sinh(ax)$
$\frac{1}{a}.sinh(ax)$	$cosh(ax)$
$\frac{1}{a}.Ln[cosh\left(ax\right)]$	$tanh(ax)$
$\frac{1}{a}.Ln\left[sinh\left(ax\right)\right]$	$coth(ax)$
$\frac{1}{a}.sin^{-1}(tanh\left(ax\right))$	$sech(ax)$
$\frac{1}{a}.Ln\left(tanh\left(\frac{ax}{2}\right)\right)$	$csch(ax)$
$\frac{1}{a}.tanh(ax)$	$sech^2\left(ax\right)$
$\frac{-1}{a}.\mathrm{cot}{\mathrm{h} \left(ax\right)\ }$	$csch^2\left(ax\right)$
$\frac{1}{a}.[ax-tanh\left(ax\right)]$	$tanh^2(ax)$
$\frac{1}{a}.[ax-coth\left(ax\right)]$	$coth^2(ax)$
$\frac{1}{2a}.\left[\frac{1}{2}sinh\left(ax\right)-ax\right]$	$sinh^2(ax)$
$\frac{1}{2a}.\left[\frac{1}{2}sinh\left(ax\right)+ax\right]$	$cosh^2(ax)$
$\frac{-1}{a}.\mathrm{sec}{\mathrm{h} \left(ax\right)\ }$	$sech\left(ax\right).tanh(ax)$
$\frac{-1}{a}.\mathrm{csc}{\mathrm{h} \left(ax\right)\ }$	$csch\left(ax\right).coth(ax)$

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

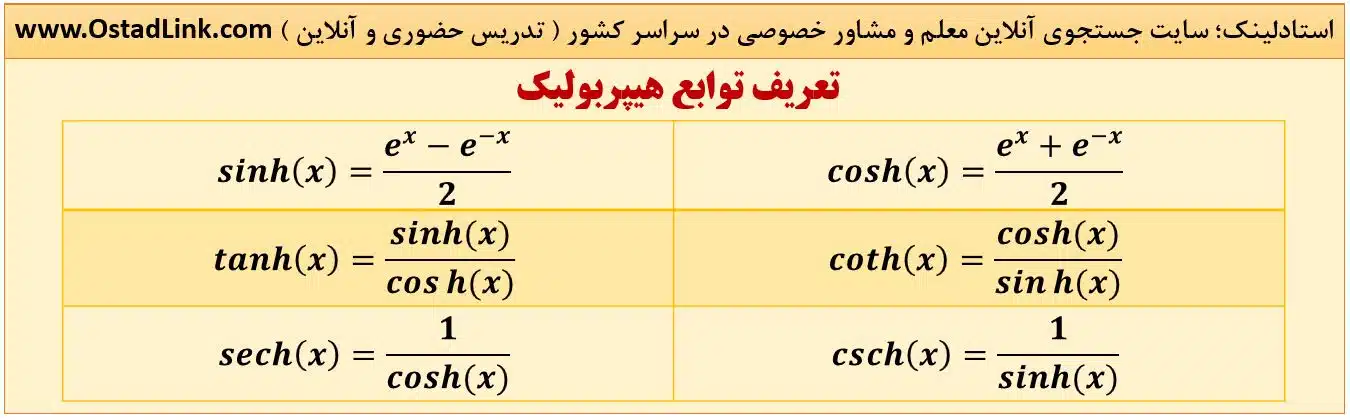
تعریف توابع هیپربولیک

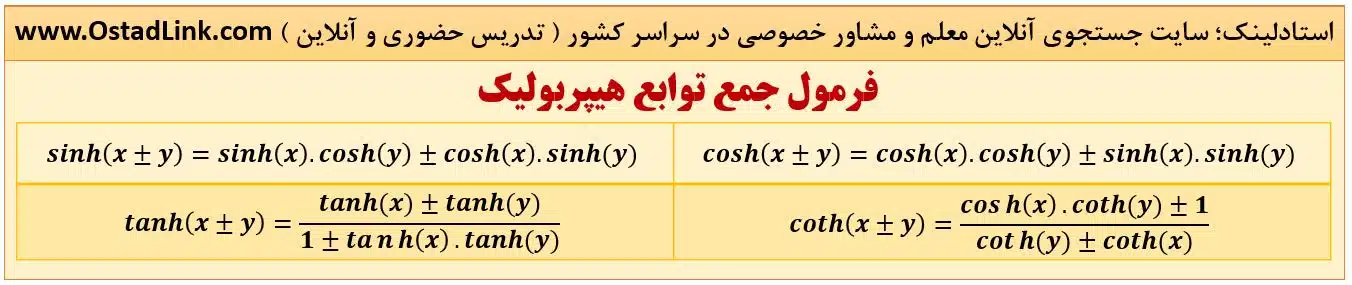
فرمول جمع کمان توابع هیپربولیک

فرمول دو برابر کمان توابع هیپربولیک

فرمول روابط میان توابع هیپربولیک

فرمول انتگرال تابع معکوس هیپربولیک

$\int{\boldsymbol{f}\left(\boldsymbol{x}\right)\boldsymbol{dx}}$	$\boldsymbol{f}\left(\boldsymbol{x}\right)$
$x.si{nh}^{-1}\left(\frac{x}{a}\right)-\sqrt{a^2+x^2}$	$si{nh}^{-1}\left(\frac{x}{a}\right)$
$x.~{cosh}^{-1}\left(\frac{x}{a}\right)\mp \sqrt{x^2-a^2}$	${cosh}^{-1}\left(\frac{x}{a}\right)$
$x.~{tanh}^{-1}\left(\frac{x}{a}\right)+\frac{a}{2}.Ln\left(a^2-x^2\right)$	$ta{nh}^{-1}\left(\frac{x}{a}\right)$
$x.~{coth}^{-1}\left(\frac{x}{a}\right)+\frac{a}{2}.Ln\left(x^2-a^2\right)$	${coth}^{-1}\left(\frac{x}{a}\right)$
$x.sech^{-1}\left(\frac{x}{a}\right)\pm a.sin^{-1}\left(\frac{x}{a}\right)$	${sech}^{-1}\left(\frac{x}{a}\right)$
${x.csch}^{-1}\left(\frac{x}{a}\right)\pm a.si{nh}^{-1}\left(\frac{x}{a}\right)$	${csch}^{-1}\left(\frac{x}{a}\right)$

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

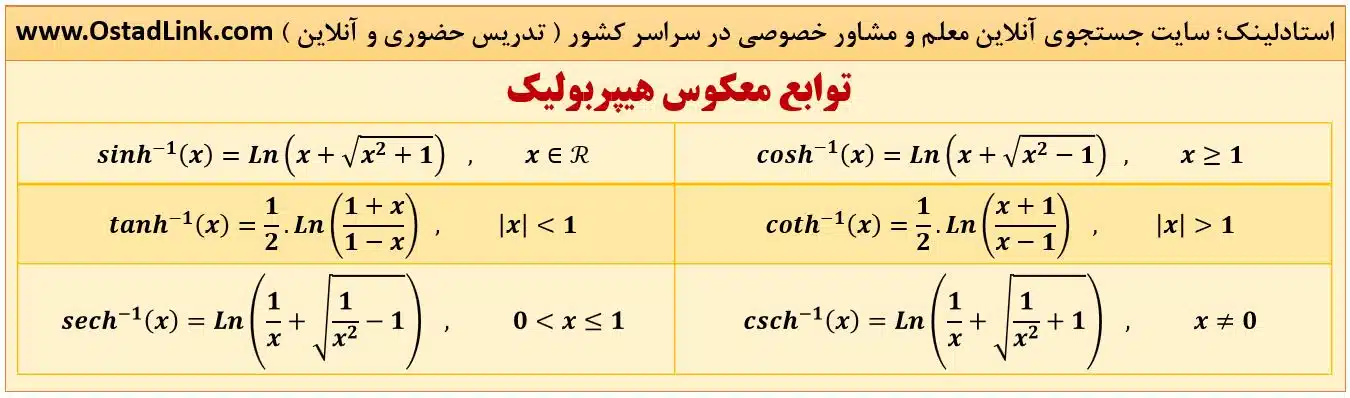
وارون ( معکوس ) توابع هیپربولیک

فرمول انتگرال توابع کسری

$\int{\boldsymbol{f}\left(\boldsymbol{x}\right)\boldsymbol{dx}}$	$\boldsymbol{f}\left(\boldsymbol{x}\right)$
$\frac{1}{a}.Ln(ax+b)$	$\frac{1}{ax+b}$
$\frac{1}{a}.tan^{-1}(\frac{x}{a})$	$\frac{1}{x^2+a^2}$
$\frac{1}{2a}.Ln(\frac{x-a}{x+a})$	$\frac{1}{x^2-a^2}$
$\frac{1}{2a}.Ln(\frac{x+a}{x-a})$	$\frac{1}{a^2-x^2}$
$sin^{-1}(\frac{x}{a})$	$\frac{1}{\sqrt{a^2-x^2}}$
$si{nh}^{-1}(\frac{x}{a})$	$\frac{1}{\sqrt{a^2+x^2}}$
$Ln(x+\sqrt{x^2-a^2})$	$\frac{1}{\sqrt{x^2-a^2}}$
$\frac{1}{a}.sec^{-1}\left\|\frac{x}{a}\right\|$	$\frac{1}{x\sqrt{x^2-a^2}}$
$-\frac{1}{a}.Ln\left(\frac{a+\sqrt{x^2+a^2}}{x}\right)$	$\frac{1}{x\sqrt{x^2+a^2}}$
$-\frac{1}{a}.Ln(\frac{a+\sqrt{a^2-x^2}}{x})$	$\frac{1}{x\sqrt{a^2-x^2}}$
$\frac{1}{bp-aq}.Ln\left(\frac{px+q}{ax+b}\right)$	$\frac{1}{\left(ax+b\right).\left(px+q\right)}$