دانلود تمامی فرمولهای کنکوری مثلثات سال دهم + فیلم آموزشی رایگان

متوسطه دوم
در مهر 1402
مطالعه 3 دقیقه

دانلود تمامی فرمولهای کنکوری مثلثات سال دهم + فیلم آموزشی رایگان

متوسطه دوم
فروردین 1401
مطالعه 3 دقیقه

در این مقاله آموزشی، تمامی فرمولهای کنکوری مثلثات سال دهم رشتۀ تجربی و ریاضی که برای کنکور و امتحانات زیاضی 1 مدارس مناسب است، آموزش داده شده است.

توجه: برای مشاهدۀ صحیح فرمول ها، در صورت استفاده از تلفن همراه، آنرا به صورت افقی قرار داده و موبایل خود را در حالت روشن ( light ) بگذارید.

دانلود جزوه تمامی فرمول های مثلثات دبیرستان و کنکور

دانلود جزوه کامل ( تایپی ) فرمول های مثلثات ویژۀ کنکور و امتحانات

فیلم آموزشی فرمول های کنکوری مثلثات

این آموزش توسط اساتید ریاضی سایت استادلینک برای شما عزیزان تهیه شده است. استادلینک، جامع ترین سایت جستجوی معلم و مشاور خصوصی در سراسر کشور می باشد که شما می توانید با مراجعه به صفحه اصلی سایت استادلینک، لیست بهترین دبیران را همراه رزومه، سابقه تدریس، فیلم نمونه آموزش و جزوات و نظر سایر شاگردان وی مشاهده نمایید و مستقیم با دبیر خصوصی خود ارتباط بگیرید.

همچنین می توانید برای رزرو معلم خصوصی ریاضی خود، از طریق پشتیبانی واتساپ استادلینک، درخواست خود را ارسال نمایید و مشاوره ما نیز بهره مند شوید.

فرمولهای کنکوری مثلثات سال دهم

کتاب ریاضی سال دهم در دو رشتۀ ریاضی و رشتۀ تجربی مشترک بوده و فرمولهایی که در زیر بیان می شود، برای هر دو رشته مشترک هستند. در جدول زیر می توانید فرمول های مثلثاتی سال دهم را مشاهده نمایید.

دامنه	فرمول	ردیف
$\alpha \neq \frac{\left(2k-1\right)\pi }{2}$	${\mathrm{tan} \left(\alpha \right)\ }=\frac{{\mathrm{sin} \left(\alpha \right)\ }}{{\mathrm{cos} \left(\alpha \right)\ }}\$	1
$\alpha \neq k\pi$	${\mathrm{cot} \left(\alpha \right)\ }=\frac{{\mathrm{cos} \left(\alpha \right)\ }}{{\mathrm{sin} \left(\alpha \right)\ }}\$	2
$\alpha \neq \frac{k\pi }{2}$	${\mathrm{tan} \left(\alpha \right)\ }\times {\mathrm{cot} \left(\alpha \right)\ }=1\$	3
$\mathcal{R}$	${sin}^2\left(\alpha \right)+{cos}^2\left(\alpha \right)=1$	4
$\mathcal{R}$	${sin}^3\left(\alpha \right)\pm {cos}^3\left(\alpha \right)=\left[{\mathrm{sin} \left(\alpha \right)\ }\pm {\mathrm{cos} \left(\alpha \right)\ }\right].[1\mp {\mathrm{sin} \left(\alpha \right)\ }.\mathrm{cos}\mathrm{}(\alpha )]$	5
$\mathcal{R}$	${sin}^4\left(\alpha \right)+{cos}^4\left(\alpha \right)=1-2\times {\left[{\mathrm{sin} \left(\alpha \right)\ }.\mathrm{cos}\mathrm{}(\alpha )\right]}^2$	6
$\mathcal{R}$	${sin}^6\left(\alpha \right)+{cos}^6\left(\alpha \right)=1-3\times {\left[{\mathrm{sin} \left(\alpha \right)\ }.\mathrm{cos}\mathrm{}(\alpha )\right]}^2$	7
$\mathcal{R}$	$\|\mathrm{sin}\mathrm{}(\alpha )\pm \mathrm{cos}\mathrm{}(\alpha )\|=\sqrt{1\pm 2{\mathrm{sin} \left(\alpha \right)\ }.\mathrm{cos}\mathrm{}(\alpha )}$	8
$\alpha \neq \frac{k\pi }{2}$	${\mathrm{tan} \left(\alpha \right)+{\mathrm{cot} \left(\alpha \right)\ }\ }=\frac{1}{{\mathrm{sin} \left(\alpha \right)\ }.{\mathrm{cos} \left(\alpha \right)\ }}\$	9
$\alpha \neq \frac{k\pi }{2}$	${tan}^2\left(\alpha \right)+{cot}^2\left(\alpha \right)={\left[{\mathrm{tan} \left(\alpha \right)\ }\pm {\mathrm{cot} \left(\alpha \right)\ }\right]}^2\mp 2$	10
$\alpha \neq \frac{k\pi }{2}$	${tan}^3\left(\alpha \right)+{cot}^3\left(\alpha \right)={\left[{\mathrm{tan} \left(\alpha \right)\ }+{\mathrm{cot} \left(\alpha \right)\ }\right]}^3-3[{\mathrm{tan} \left(\alpha \right)+\mathrm{cot}\mathrm{}(\alpha )\ }]$	11
$\alpha \neq \frac{k\pi }{2}$	$\frac{1+\mathrm{tan}\mathrm{}(\alpha )}{1+\mathrm{cot}\mathrm{}(\alpha )}=\mathrm{tan}\mathrm{}(\alpha )$	12

توجه: ستون دامنه در جدول بالا، مربوط به فرمولهای مثلثات سال دوازدهم می باشد.

دانلود تمامی فرمول های کنکوری مثلثات دبیرستان

در این بخش می توانید PDF فرمول های مثلثات ویژۀ کنکور و امتحانات را از سایت تدریس خصوصی استادلینک دانلود نمایید. برای دانلود جزوه کامل فرمول های مثلثات، کافی است روی عبارت زیر ضربه بزنید.

دانلود جزوه کامل ( تایپی ) فرمول های مثلثات ویژۀ کنکور و امتحانات

زاویه های متمم در مثلثات

نکته: در زبان انگلیسی، هر موقع حرف “co” به اول واژه اضافه شود، معنای شبیه و همزاد به آن واژه اضافه می کند. مثلا اگر به اول واژۀ “انرژی”، واژۀ “کو” اضافه شود ( کو انرژی ) معنای آن، شبیه انرژی می شود. حالا به دو عبارت زیر دقت کنید:

کوسینوس = co+sin —> شبیه سینوس
کوتانژانت = co + tan —> شبیه تانژانت

پس می توان نتیجه گرفت که کوسینوس و سینوس همزاد هم بوده و تانژانت و کوتانژات نیز همزاد هم هستند.

یادآوری: دو زاویه را متمم هم گویند، هرگاه مجموع آنها برابر 90 درجه شود.

با توجه به تصویر بالا، می توان نتیجه گرفت در مثلثات، سینوس یک زاوبه، با کسینوس زاویۀ متمم آن برابر است و همچنین تانژانت یک زاویه، با کوتانژانت زاویۀ متمم آن برابر است. به عنوان مثال داریم:

${\mathrm{tan} \left(37\right)\ }={\mathrm{cot} \left(53\right)\ }=\frac{3}{4}$

${\mathrm{sin} \left(30\right)\ }={\mathrm{cos} \left(60\right)\ }=\frac{1}{2}$

دایره مثلثاتی

نسبت های مثلثاتی، علاوه بر مثلث قائم الزاویه، در دایرۀ مثلثاتی نیز تعریف می شوند. دایرۀ مثلثاتی، یک دایره به شعاع واحد ( شعاع یک ) بوده که مطابق شکل زیر به چهار ناحیه یا چهار ربع تقسیم میشود.

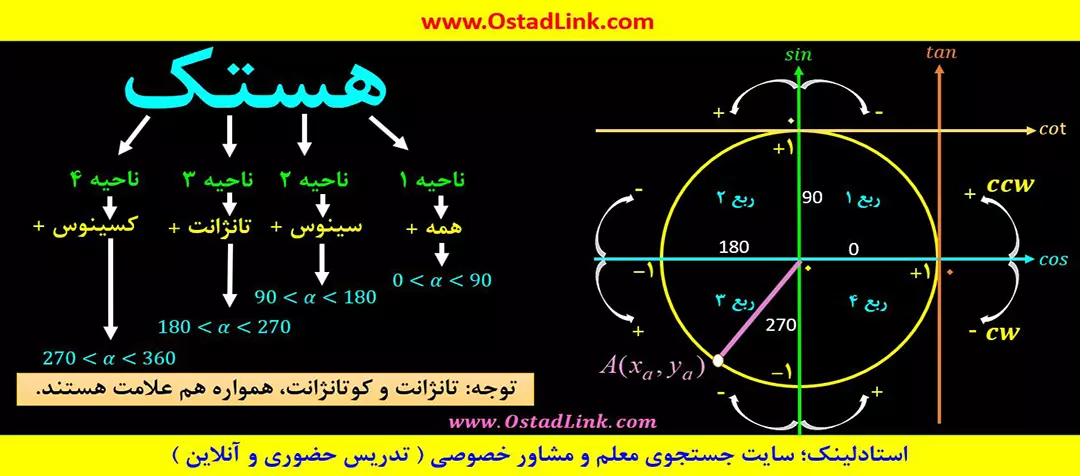
توجه1: اگر نقطۀ A(x,y) بخواهید روی دایرۀ مثلثاتی باشد، باید در رابطۀ زیر صدق کند.

$A\left(x_a,y_a\right)\to x^2_a+y^2_a=1$

توجه2: اگر نقطۀ A(x,y) روی دایرۀ مثلثاتی باشد، روبط زیر بر آن حاکم است.

${\mathrm{sin} \left(\alpha \right)\ }=y_a$	${\mathrm{cos} \left(\alpha \right)\ }=x_a$
${\mathrm{cot} \left(\alpha \right)\ }=\frac{x_a}{y_a}$	${\mathrm{tan} \left(\alpha \right)\ }=\frac{y_a}{x_a}$

توجه3: سینوس و کسینوس چون در داخل دایرۀ مثلثاتی هستند، همواره بین 1- تا 1 بوده و تانژانت و کوتانژانت بخاطر اینکه مماس به دایرۀ مثلثاتی هستند و خارج آن قرار دارند، می توانند هر عددی را اختیار کنند.

$-1\le \mathrm{cos}\mathrm{}(\alpha )\le 1$	$-1\le \mathrm{sin}\mathrm{}(\alpha )\le 1$
$-\infty <\mathrm{cot}\mathrm{}(\alpha )<+\infty$	$-\infty <{\mathrm{tan} \left(\alpha \right)\ }<+\infty$

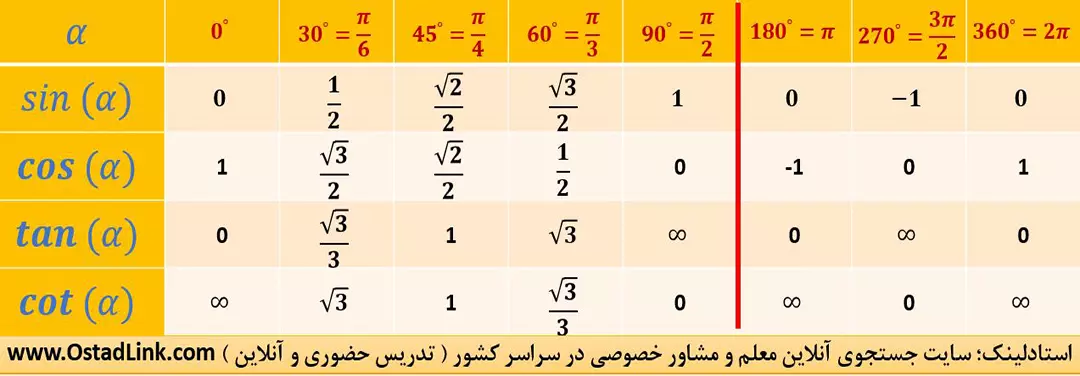
جدول زاویه ها در مثلثات

در جدول زیر، زاویه های مهمی که باید نسبت های مثلثاتی آنرا بدانید، آورده شده است.

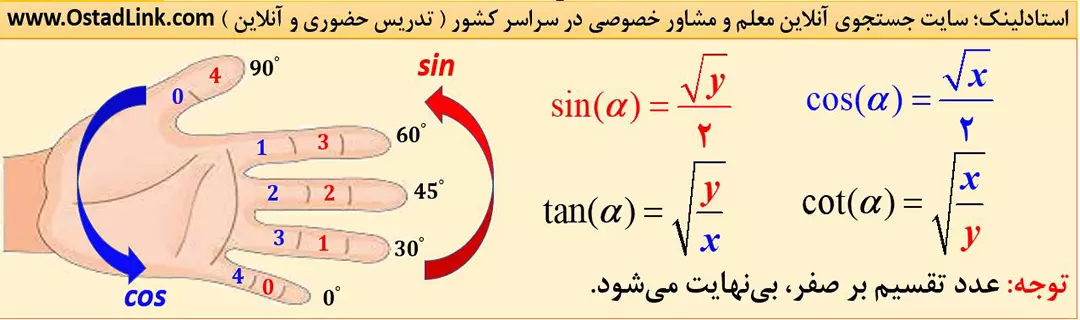
در عکس زیر، به کمک قاعدۀ دست چپ، میتوان نسبت های مثلثاتی زاویۀ صفر تا 90 درجه را به راحتی محاسبه کرد.

قانون سینوس ها

قانون سینوس ها، در محاسبۀ مساحت ها، در رابطۀ بین سه ضلع و سه زاویۀ یک مثلث و همچنین محاسبۀ رابطۀ بین سه نیروی متعادل، کاربرد دارد. مورد اول به طور غیر مستقیم در کتاب ریاضی دهم اشاره شده و دو مورد آخر در کتاب هندسه 2 سال یازدهم رشتۀ ریاضی بیان شده است.

قانون سینوس ها در مساحت ها:

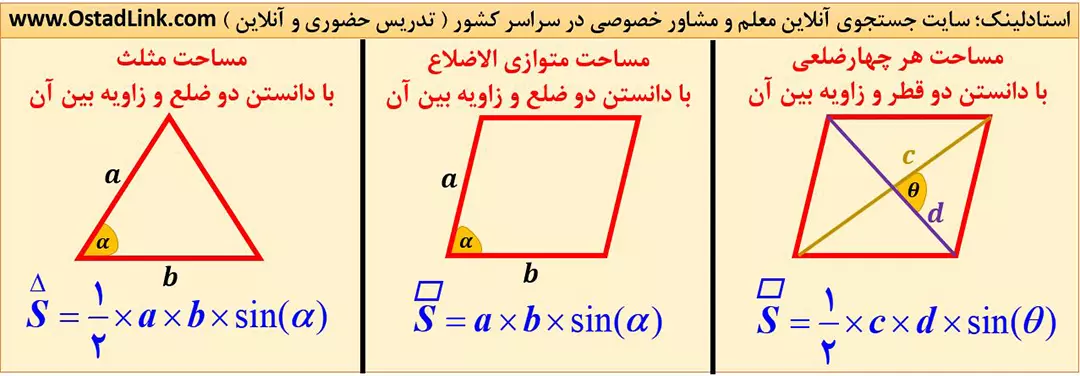
در تصویر زیر، مساحتی از شکل های پر تکرار کتاب درسی که در کنکور و سوالات تستی، پر تکرار هستند را بیان کرده ایم.

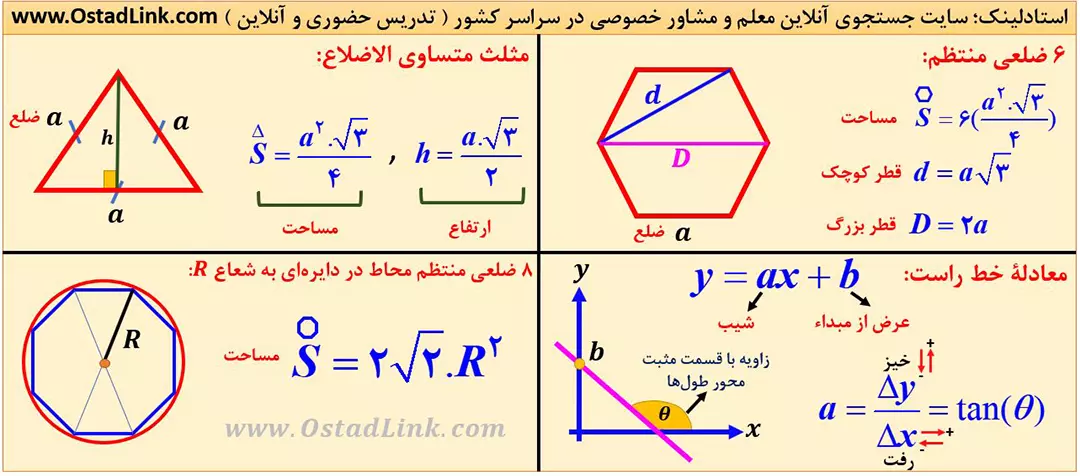
اگر احتیاج به معلم خصوصی ریاضی دارید، همین الان از طریق پشتیبانی واتساپ سایت استادلینک، درخواست معلم خصوصی ریاضی خود را ارسال نمایید. برای این منظور، نام و نام خانوادگی، مقطع تحصیلی، درس مورد نیاز به همراه نام ” استادلینک ” را داخل واتساپ ارسال نمایید.