آموزش سری فوریه | دانلود جزوه کامل جدول خواص سری فوریه

در این مقاله با آموزش جامع سری فوریه و خواص سری فوریه آشنا می شوید و همچنین می توانید جزوه کامل سری فوریه را دانلود نمایید. سایت کلاس خصوصی استادلینک

استادلینک؛ جامع ترین سایت انتحاب معلم و استاد خصوصی در سراسر کشور بوده که با مراجعه به صفحه اصلی سایت استادلینک، می توانید رزومخ و سوابق تحصیل و فیلم نمونه تدریس برترین اساتید را مشاهده کرده و با آنها کلاس خصوصی برگزار کنید.

دانلود جزوه آموزش سری فوریه و خواص آن

سری فوریه توابع پیوسته

تابع پیوسته و متناوب f(t) با دورۀ تناوب T را در نظر بگیرید. سری فوریه برای این تابع به دو صورت حقیقی و بر اساس پایه های سینوسی و کسینوسی و همچنین به صورت سری فوریه مختلط تعریف می شود که در ادامه با هر دوی آنها آشنا می شویم.

قبل از مطالعه این بخش حتماً « آموزش جامع انتگرال جز به جز » را مشاهده نمایید.

توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.

سری فوریه حقیقی

اثبات می شود که می توان تابع متناوب f(t) با دورۀ تناوب T را بر حسب پایه های سینوس و کسینوس به صورت زیر نوشت:

$f\left(t\right)=a_0+\sum^{n=\infty }_{n=1}{\left[a_n.{cos \left(n\omega t\right)\ }+b_n.{sin \left(n\omega t\right)\ }\right]}$

که به a₀ و a_n و b_n، ضرائب سری فوریه گفته می شوند که a_n و b_n خود دو تابع گسسته است و همچنین به w، اُمگا یا فرکانس زاویه می گویند که به صورت زیر تعرفی می شود:

$\omega =\frac{2\pi }{T}$

فرمول محاسبه ضرائب سری فوریه

اگر سری فوریه را به صورت بالا تعریف کنیم، ضرائب آن به صورت زیر محاسبه می شود:

$a_0=\frac{1}{T}\int^{\ }_T{f\left(t\right)dt}$

$a_n=\frac{2}{T}\int^{\ }_T{f\left(t\right).{cos \left(n\omega t\right)\ }dt}$

$b_n=\frac{2}{T}\int^{\ }_T{f\left(t\right).{sin \left(n\omega t\right)\ }dt}$

که به a₀ مقدار متوسط یا مقدار dc تابع f(t) گفته می شود و به a₁ و b₁ ضرائب هارمونیک اول یا هارمونیک اصلی گفته می شود که در مهندسی برق بسیار کاربرد دارد.

توجه: بازۀ انتگرال گیری باید در یک دورۀ تناوب باشد و الزماً از 0 تا T نیست.

نمایش دیگر سری فوریه

در برخی از مراجع، سری فوریه را به صورت زیر تعریف می کنند:

$f\left(t\right)=\frac{a_0}{2}+\sum^{n=\infty }_{n=1}{\left[a_n.{cos \left(n\omega t\right)\ }+b_n.{sin \left(n\omega t\right)\ }\right]}$

در این حالت، ضریب a₀ به صورت زیر بدست می آید:

$a_0=\frac{2}{T}\int^{\ }_T{f\left(t\right)dt}$

در این حالت، به نصف a₀ مقدار dc می گویند.

چند نکته مهم در مورد ضرائب سری فوریه

برای رزرو استاد خصوصی درس مورد نظر خود می توانید از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

نکتۀ 1: اثبات می شود که a_n تابعی زوج است و b_n تابعی فرد است.

نکتۀ 2: اگر f(t) تایعی زوج باشد و دامنۀ متقارن داشته باشد، اثبات می شود که b_n=0 می شود.

نکتۀ 3: اگر f(t) تابعی فرد باشد و دامنۀ متقارن داشته باشد، اثبات می شود که a_n=a₀=0 می شود.

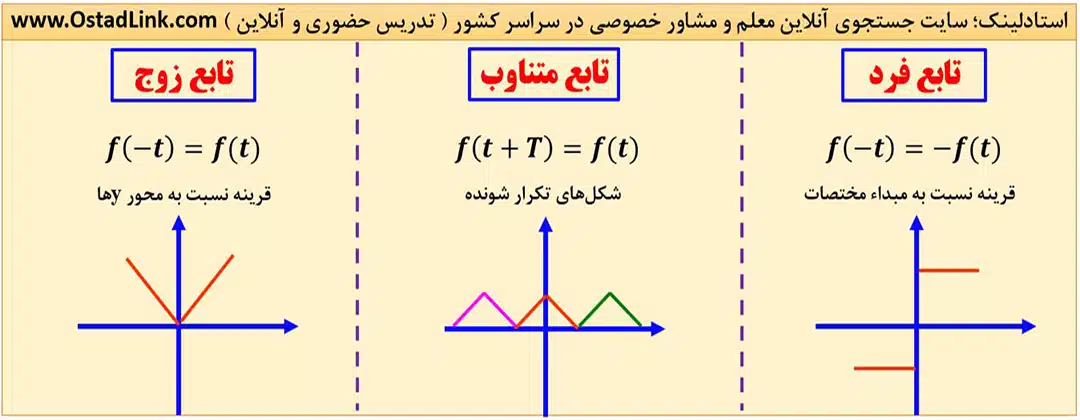
سری فوریه مختلط

قبل ار بیان سری فوریه مختلط، ابتدا چند یادآوری ریاضی با هم داشته باشیم:

الف) نماد اعداد مختلط:

$i=j=\sqrt{-1}$

ب) رابطۀ اویلر:

$e^{j\alpha }={cos \left(\alpha \right)\ }+jsin(\alpha )$

$e^{-j\alpha }={\mathrm{cos} \left(\alpha \right)\ }-jsin(\alpha )$

برای رزرو استاد خصوصی درس مورد نظر خود می توانید از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

سری فوریه مختلط

نمایش آن به صورت زیر است:

$f\left(t\right)=\sum^{n=\infty }_{n=-\infty }{c_n.e^{j.n.\omega .t}}$

که c_n ضریب سری فوریه مختلط می باشد و به صورت زیر محاسبه می شود:

$c_n=\frac{1}{T}\int^{\ }_{T\ }{f\left(t\right).e^{-j.n.\omega .t}dt}$

رابطه میان ضرائب سری فوری حقیقی و مختلط

به راحتی با مقایسۀ فرمول c_n با فرمول a_n و b_n می توان دریافت که:

$c_0=a_0$

$c_n=\frac{a_n-jb_n}{2}$

از طرفی می توان رابطۀ بالا را به صورت زیر نوشت:

$a_n=2.Re\left\{c_n\right\}$

$b_n=-2.Im\left\{c_n\right\}$

منظور از Re قسمت حقیقی (Real) و منظور از Im قسمت موهومی (Image) است.

توجه: c_n یک تابع گسستۀ مختلط است که قسمت حقیقی آن، یک تابع زوج و قسمت موهومی آن، یک تایع فرد می باشد.

برای رزرو استاد خصوصی درس مورد نظر خود می توانید از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

خواص سری فوریه (Fourier Series)

توجه: این خواص برای سری فوریه مختلط بیان می شود.

فرض کنید دو تایع متناوب و پیوستۀ f(t) و g(t) که هر دو دارای دورۀ تناوب T هستند، دارای ضرائب سری فوریۀ c_n و d_n باشند، داریم:

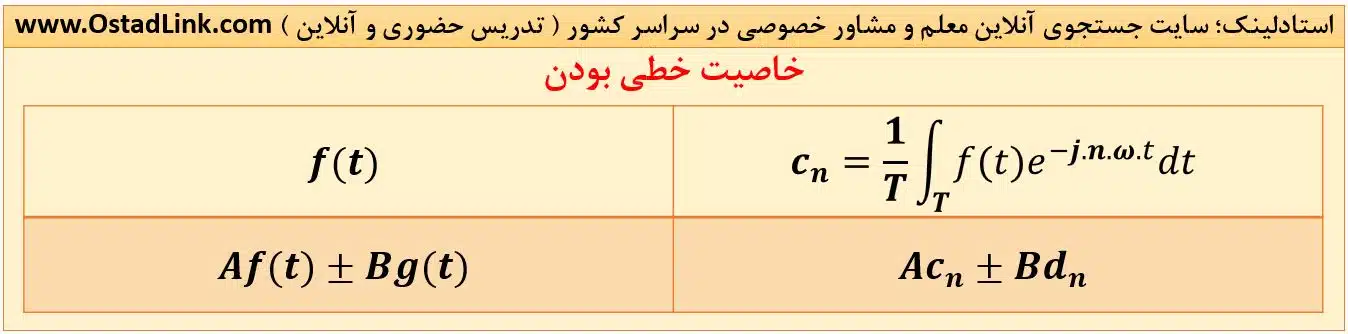
1- خاصیت خطی

خاصیت خطی یعنی همزمان همگن و جمع پذیر بودن. اگر دو تابع f(t) و g(t) دارای یک دوره تناوب باشند داریم:

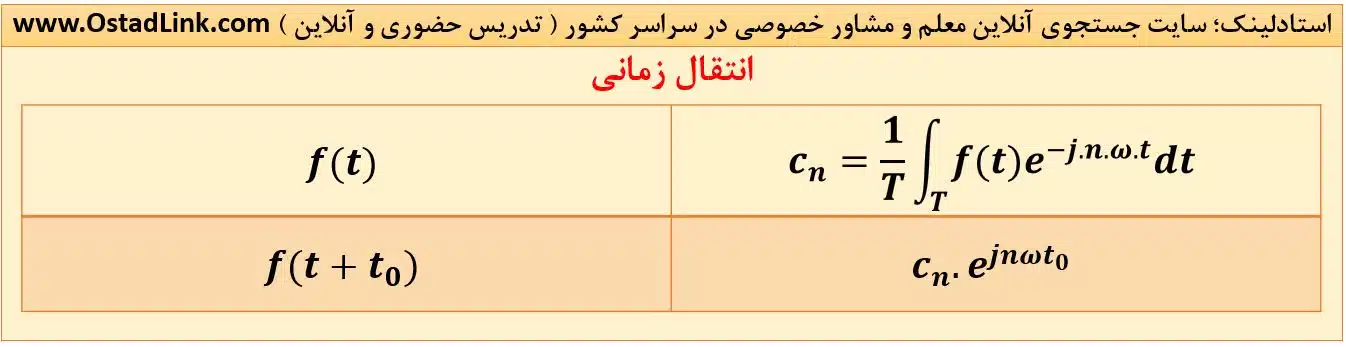
2- انتقال زمانی

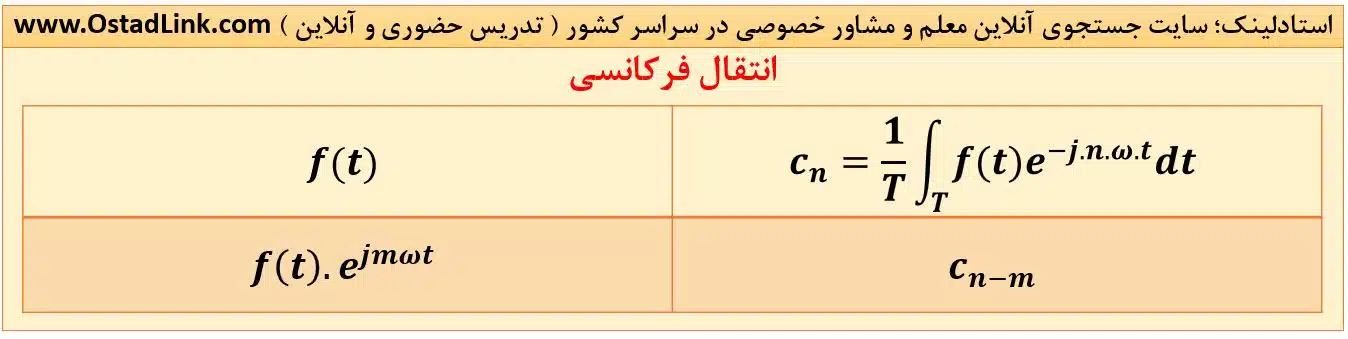
3- انتقال فرکانسی

به شرط آنکه m عضو اعداد صحیح باشد داریم:

4- وارونگی

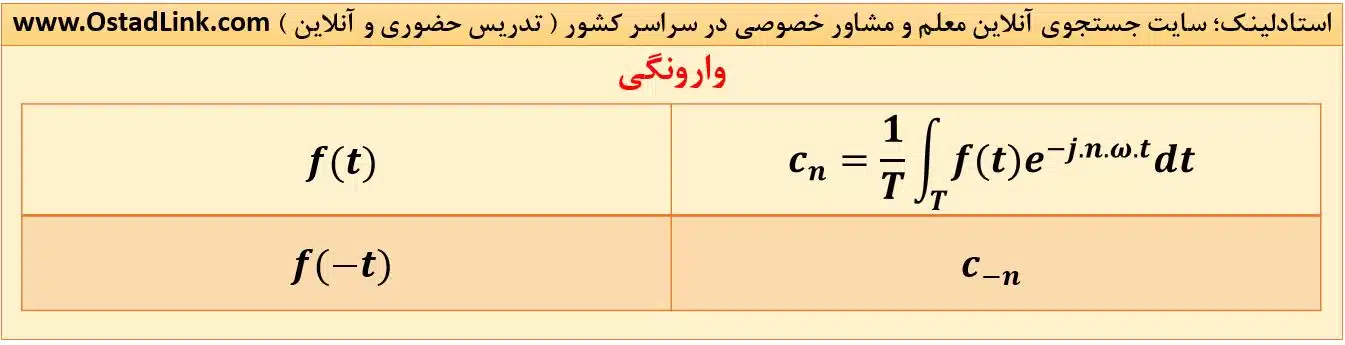
5- مزدوجی

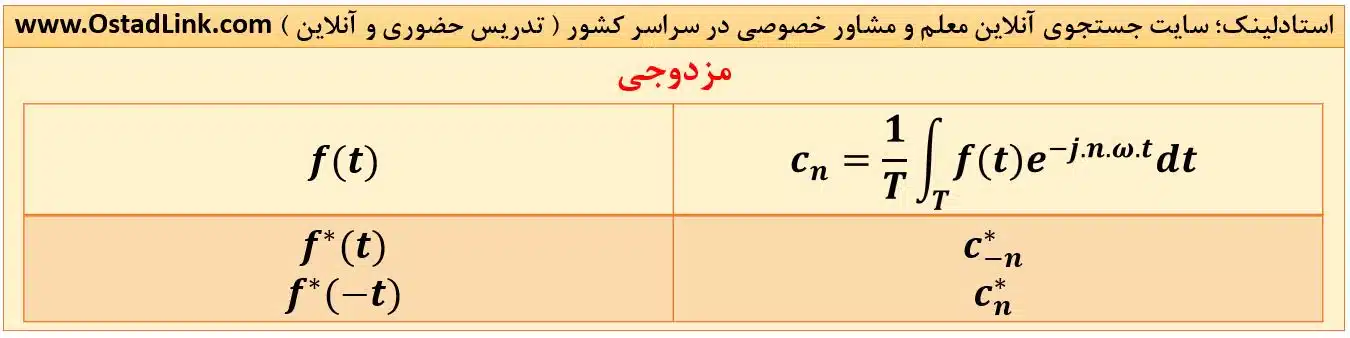
6- مقیاس دهی زمانی

به شرط آنکه a عددی مثبت باشد داریم:

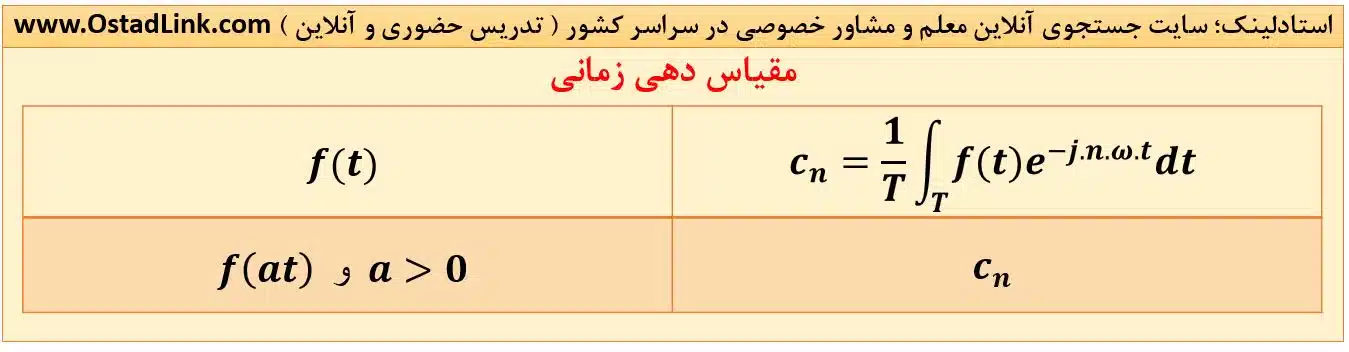
7- کانولوشن متناوب در زمان

به شرط آنکه دو تابع f(t) و g(t) دارای یک دوره تناوب (T) باشند داریم:

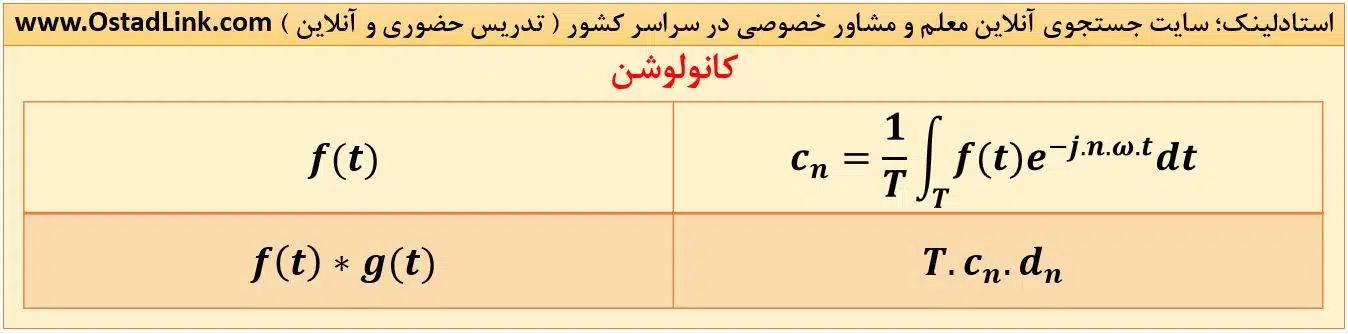
برای مطالعه خواص کانولوشن و فرمول های آن، اینجا ضربه بزنید.

8- ضرب در حوزه زمان

به شرط آنکه دو تابع f(t) و g(t) دارای یک دوره تناوب (T) باشند داریم:

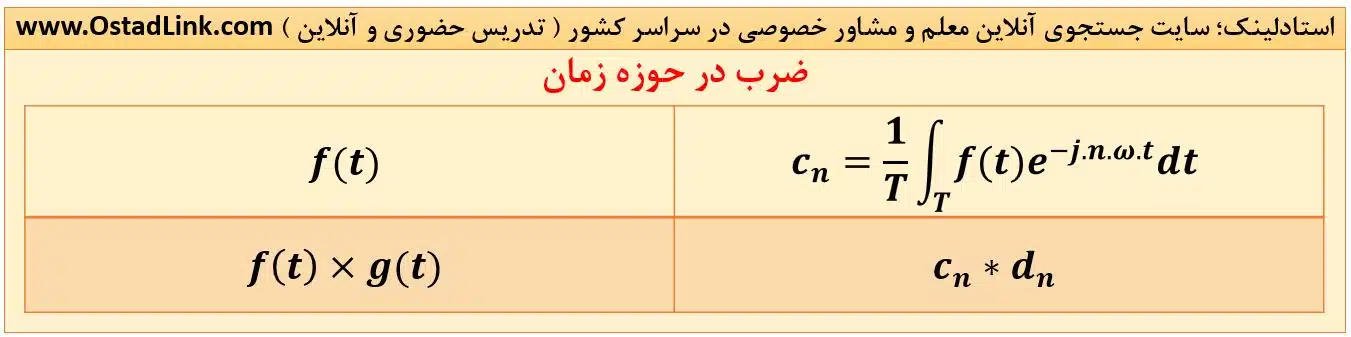
9- مشتق گیری در زمان

برای تابع پیوسته رابطۀ زیر را داریم:

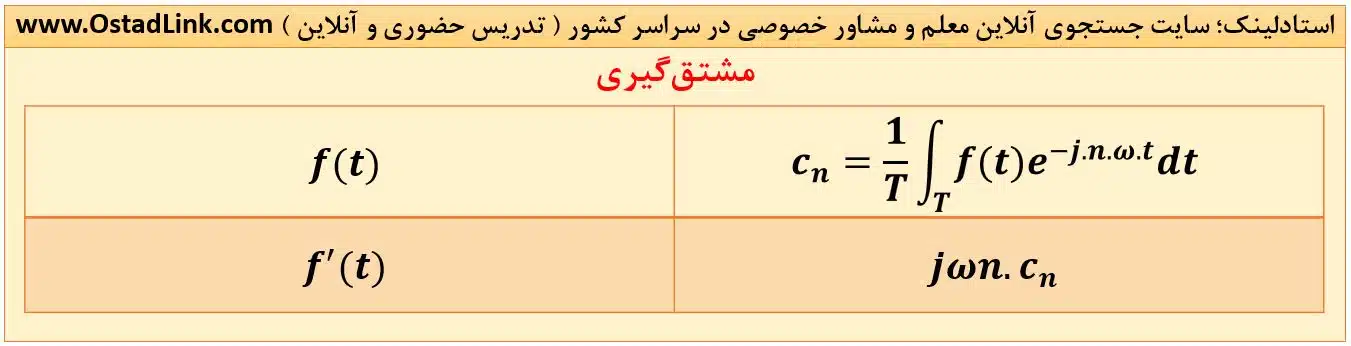
اما در تابع گسسته x[n] با ضریب سری فوریه c_k و دورۀ تناوب N، رابطه به صورت زیر اصلاح می شود:

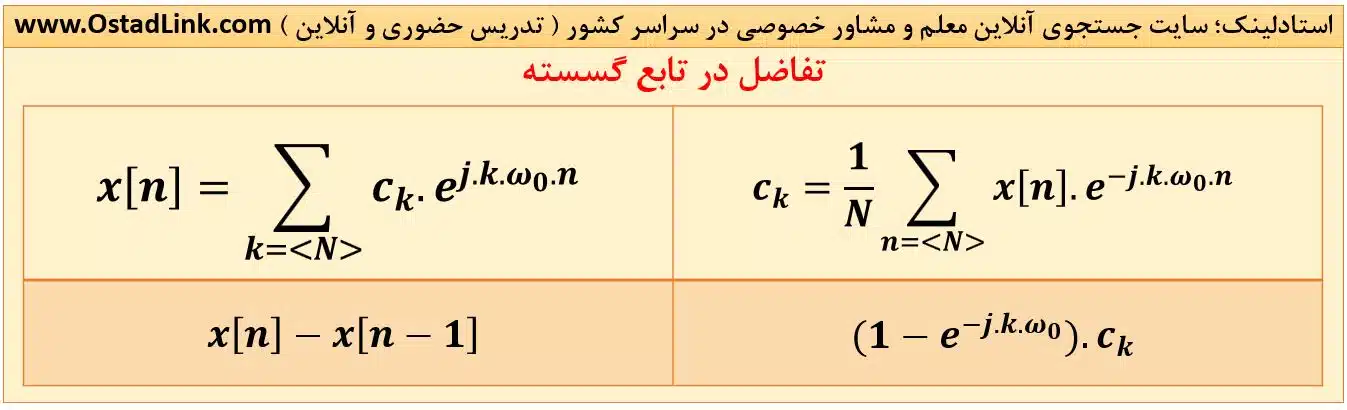
که w₀ همان فرکانس زاویه است که به صورت زیر در تابع گسسته تعریف می شود:

${\omega }_0=\frac{2\pi }{N}$

توجه: چون N یک عدد طبیعی ( صحیح ) است، پس w₀ نمی تواند هر مقداری را اختیار کند و مقدار زیر باید یک مقدار صحیح باشد:

$N=\frac{2\pi }{{\omega }_0}$

برای رزرو استاد خصوصی درس مورد نظر خود می توانید از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

10- رابطه پارسوال

رابطه پارسوال برای تابع پیوسته به صورت زیر تعریف می شود:

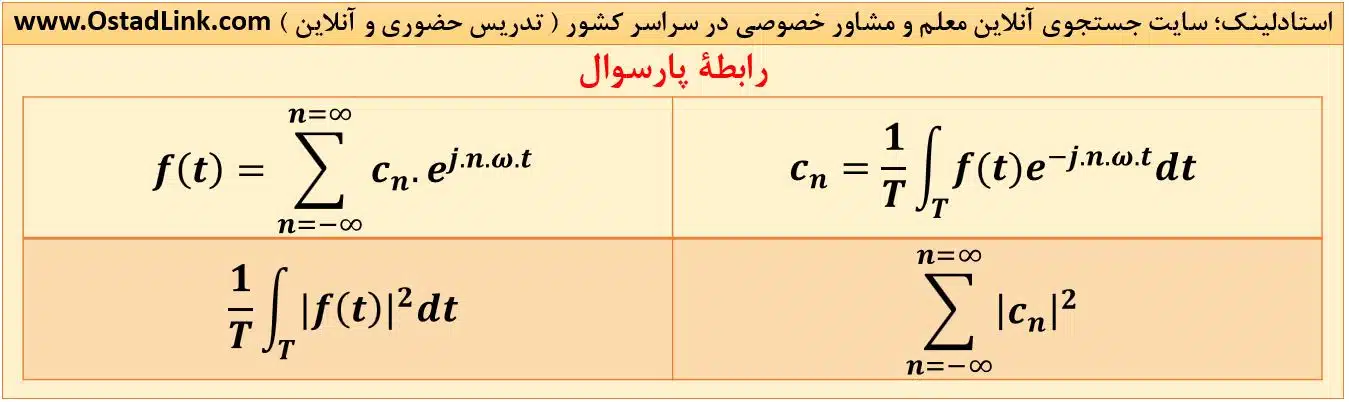
اگر سیگنال f(t) به صورت زیر تعریف شود:

$f\left(t\right)=a_0+\sum^{n=\infty }_{n=1}{\left[a_n.{cos \left(n\omega t\right)\ }+b_n.{sin \left(n\omega t\right)\ }\right]}$

رابطه پارسوال به صورت زیر تغییر می کند که این مبحث در درس ریاضیات مهندسی بسیار کاربرد دارد.

$\frac{1}{T}\int^{\ }_{T\ }{{\left|f\left(t\right)\right|}^{2\ }dt=\ a^{2\ }_0\ +\frac{1}{2}\sum^{\infty }_{n=1}{\left[a^{2\ }_n+b^{2\ }_n\right]}}$

رابطه پارسوال در سری فوریه گسسته

برای رزرو استاد خصوصی درس مورد نظر خود می توانید از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

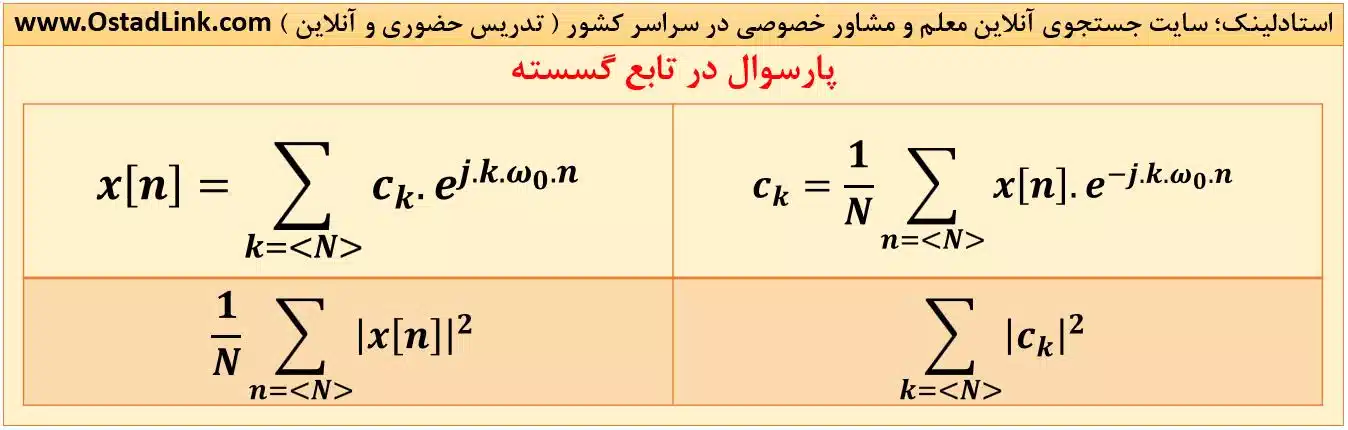
11- رابطه دوگانی در سری فوریه

انواع رابطه های دوگانی ( سری – سری )، ( تبدیل – سری ؛ نوع اول ) و ( تبدیل – سری ؛ نوع دوم ) را می توانید از جزوه آموزش جامع سری فوریه و خواص آن مشاهده کنید.

دانلود جزوه آموزش سری فوریه

در این جزوه با تمام ویژگی ها و جدول های سری فوریه آشنا می شوید. برای دانلود جزوۀ کامل سری قوریه روی جعبۀ زیر ضربه بزنید.

دانلود جزوه آموزش سری فوریه و خواص آن

مقالات مرتبط:

دانلود تمامی فرمول های مشتق (جدول های مشتق)

دانلود فرمول های کلی انتگرال گیری

آموزش جامع تبدیل فوریه و خواص آن

داغ‌ترین مطالب روز

آموزش خط به خط شیمی یازدهم فصل ۲ ( بخش 2 )

بخش 2 فصل ۲ آموزش خط به خط شیمی یازدهم شامل موارد زیر می باشد: جاری شدن انرژی گرمایی واکنش های گرماده و گرماگیر مبادلۀ گرما بر اثر انجام واکنش در دمای ثابت عوامل مؤثر بر گرمای واکنش آنتالپی مسائل استوکیومتری ΔH 6- جاری شدن انرژی گرمایی | تدریس خصوصی شیمی دانلود جزوه تمامی فرمول […]

دانلود تمامی سوالات آزمون جامع گاج انسانی نظام جدید

دانلود تمامی سوالات آزمون جامع گاج رشته علوم انسانی نظام جدید از سال 1398 تا کنون به همراه جواب و پاسخنامه تشریحی توجه: استفاده از مطالب سایت جستجوی معلم خصوصی استادلینک با درج نام منبع ( سایت استادلینک ) بلامانع می باشد. دانلود سوالات آزمون جامع گاج انسانی 1398 برای دانلود سوالات آزمون جامع گاج […]

دانلود سوالات امتحان نهایی فیزیک تجربی دوازدهم دی 97 + جواب

دانلود سوالات امتحان نهایی فیزیک دوازدهم تجربی دی 1397 همراه با پاسخنامه تشریحی + معرفی بهترین معلم خصوصی و تدریس خصوصی ویژه امتحانات نهایی رشته تجربی در ادامه با بارم بندی امتحان نهایی فیزیک 3 رشته تجربی و نحوه مطالعه صحیح این درس و راه حل پاس شدن در امتحانات نهایی و ترمیم معدل با […]