آموزش جامع انتگرال جز به جز، حل مثال از انواع انتگرال جز به جز و دانلود جزوه کامل انتگرال جز به جز از سایت تدریس خصوصی استادلینک، همگی در این مقاله آموزشی
استادلینک؛ جامع ترین وبسایت جستجوی معلم خصوصی و استاد خصوصی در سراسر کشور بوده که با مراجعه به صفحۀ اول سایت استادلینک، می توانید لیست بهترین اساتید رشته های مختلف را مشاهده کنید.
همچنین برای رزرو استاد خصوصی درس مورد نظر خود می توانید از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.
| دانلود جزوه کامل انتگرال و تمامی جدول ها و فرمول های انتگرال گیری |
قواعد دیفرانسیل ها
قبل از خواندن این مقاله، حتماً مقالۀ « آموزش جامع انتگرال انواع توابع » را مطالعه بفرمایید.
قواعد دیفرانسیل ها دقیقاً مشابه قواعد مشتق ها است.
توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.
![]()
![]()
![]()
« برای مشاهده و دانلود تمامی قواعد و فرمول های مشتق، اینجا ضربه بزنید. »
به عنوان مثال داریم:
![]()
![]()
![]()
آموزش انتگرال جز به جز نوع اول
همانطور که می دانید، به جز انتگرال های توابع گفته شده در مقالۀ « آموزش جامع انتگرال انواع توابع »، روش و قاعدۀ کلی برای انتگرال گرفتن از سایر فرمول ها وجود ندارد.
در انتگرال هایی که در آنها Ln یا tan-1 یا sin-1 ( در کل توابع معکوس مثلثاتی و ال ان و … ) وجود داشته باشد و نتوان آنها را با تغییر متغیر حل کرد، به احتمال زیاد، این انتگرال ها به کمک انتگرال جز به جز نوع اول قابل حل هستند.
فلسفه انتگرال جز به جز نوع اول:
می دانیم دیفرانسیل ضرب دو تابع به صورت زیر تعریف می شود:
![]()
این عبارت را می توان به صورت زیر باز نویسی کرد:
![]()
همانطور که می دانید، انتگرال و دیفرانسل ضد هم هستند و اگر مستقیم و بدون هیچ واسطه ای، علامت انتگرال و علامت دیفرانسیل به هم برخورد کنند، همدیگر را خنثی می کنند یعنی:
![]()
حال اگر از طرفین رابطۀ بازنویسی شده انتگرال بگیریم داریم:
![]()
رابطۀ بالا فرمول اصلی انتگرال جزء به جزء نوع اول است. چون گاهی از مواقع نمی توان انتگرال u.dv را مستقیم محاسبه کرد، پس به کمک رابطۀ بالا انتگرال v.du را محاسبه می کنیم.
چند مثال از انتگرال جز به جز نوع اول
در این نوع از انتگرال ها انتخاب قسمت u و قسمت dv مهم است. به طور کلی u قسمتی است که انتگرال آن را نمی دانیم ولی مشتق آن را می دانیم و dv مابقی قسمت انتگرل ما است. به چند مثال زیر دقت کنید.
جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

مثالی کمی سخت تر از انتگرال جزء به جزء نوع اول را در تصویر زیر مشاهده کنید.

و در آخر، یک مثال از تانژانت وارون:

جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.
آموزش انتگرال جز به جز نوع دوم
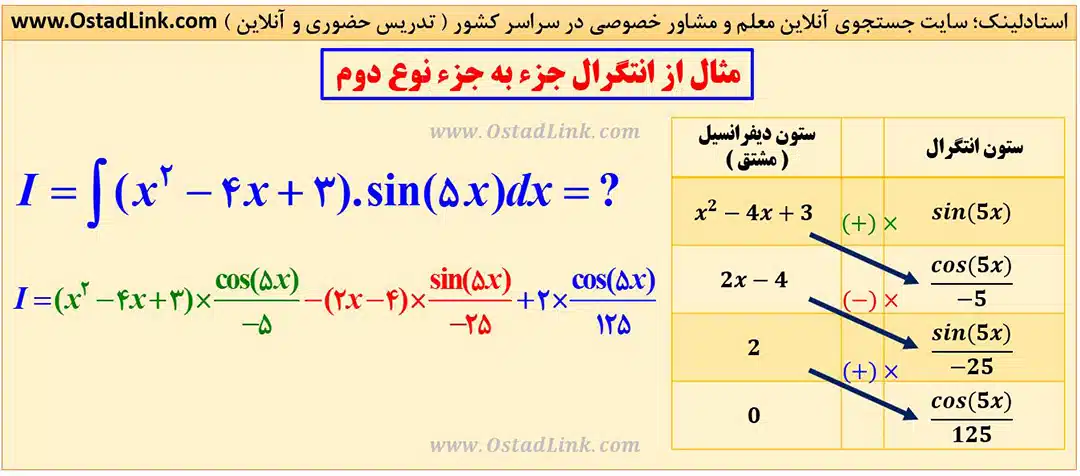
این انتگرال از ضرب بک چند جمله ای در تابع نمایی یا سینوس یا کسینوس یا توابع هیپربولیک ( sinh و cosh ) تشکیل شده است. در ستون سمت چپ جدول، قسمت مشتق پذیر یا چند جمله ای را نوشته و زیر هم مشتق متوالی گرفته تا مشتق به صفر برسد.
در ستون سمت راست، قسمت نمایی یا مثلثاتی را نوشته و انتگرال متوالی گرفته تا به روبروی صفر ستون چپ برسد و سپس به صورت اُریب، عبارات را در هم ضرب کرده و علامت آنها را یکی در میان مثب و منفی قرار می دهیم.
چند مثال از انتگرال جز به جز نوع دوم
جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.
توجه شود که حل انتگرال جز به جز نوع دوم بسیار بسیار مهم است و در محاسبات سری فوریه و تبدیل فوریه بسیار کاربرد دارد.

در مثال زیر به جای تابع نمایی، تابع سینوس قرار گرفته است.
جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.
آموزش انتگرال جز به جز نوع سوم ( انتگرال بازگشتی )
این انتگرال جز به جز از نوع انتگرال بازگشتی بوده و معمولاً از ضرب سینوس و کسینوس در تابع نمایی یا سینوس هیپربولیک و کسینوس هیپربولیک تشکیل شده است.
تابع سینوس و کسینوس را در ستون مشتق قرار داده و دوباز از آن عبارت به صورت پیاپی مشتق بگیرید و قسمت نمایی یا هیپربولیک را در ستون انتگرال قرار داده و دوبار از آن انتگرال بگیرید.
چند مثال از انتگرال جز به جز نوع سوم ( انتگرال بازگشتی )
جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

فرمول های انتگرال بازگشتی
جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.
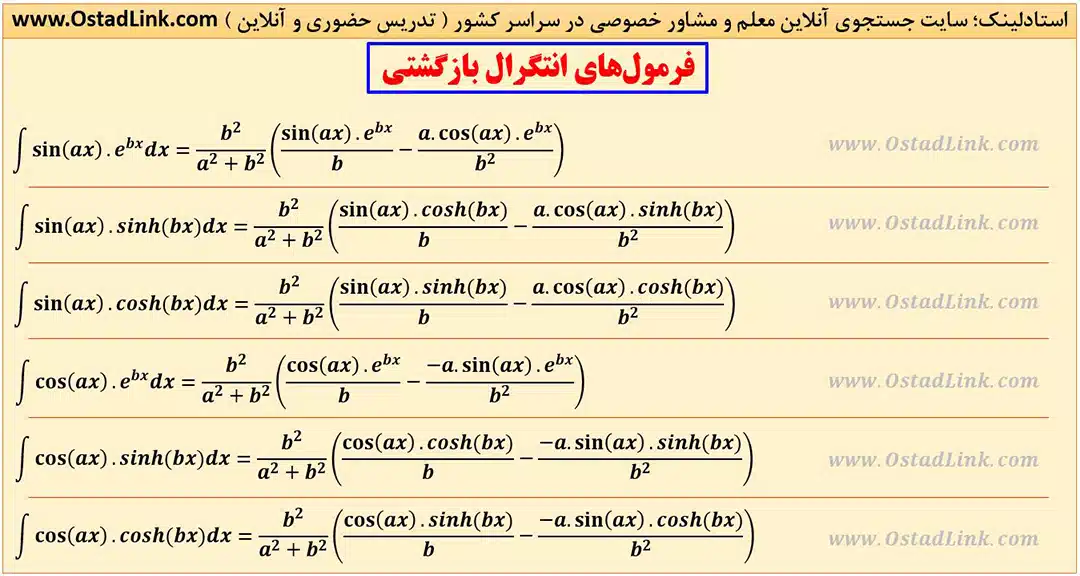
انتگرال بازگشتی مثلثاتی
جهت رزرو معلم و استاد خصوصی ریاضی ( از دبستان تا دکتری ) به پشتیبانی واتساپ سایت استادلینک پیام دهید.

مقالات مرتبط:
آموزش جامع تبدیل لاپلاس و آموزش تابع گاما




















2 پاسخ
با زبان ساده و بسیار عالی درس داده شده و واقعا مفید بود. ممنون از زحماتتون
خواهش می کنم
ممنونم که استادلینک را انتخاب کردید