آموزش تبدیل فوریه | دانلود جدول خواص تبدیل فوریه

در این مقاله با آموزش تبدیل فوریه زمان پیوسته و گسسته، دانلود جزوه کامل خواص تبدیل فوریه و همچنین تیدبل فوریه در حوزه فرکانس آشنا می شوید.

استادلینک؛ سایت انتخاب معلم و استاد خصوصی در سراسر کشور ( تدریس حضوری و آنلاین ) است که با مراجعه به صفحه اول سایت استادلینک می توانید لیست برترین اساتید کشور را به همراه رزومه و فیلم نمونه تدریس آنها مشاهده نمایید.

همچنین می توانید برای رزرو معلم و استاد خصوصی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

دانلود جزوه کامل تبدیل فوریه

تعریف تبدیل فوریه پیوسته

قبل از مطالعه این بخش حتماً « آموزش جامع انتگرال جز به جز » را مشاهده نمایید.

تبدیل فوریه برخلاف سری فوریه، برای توابع غیر متناوب بوده و در برخی مراجع تبدیل فوریه پیوسته (CTFT) به صورت زیر تعریف می شود:

توجه: اگر از تلفن همراه استفاده می نمایید، آن را در حالت روشن (light) و در وضعیت افقی قرار داده تا فرمول ها برای شما به درستی به نمایش در آید.

$X\left(\omega \right)=\int^{+\infty }_{-\infty }{x\left(t\right).e^{-j\omega t}dt}$

در این عکس تبدیل فوریه به صورت زیر تعریف می شود:

$x\left(t\right)=\frac{1}{2\pi }\int^{+\infty }_{-\infty }{X\left(\omega \right).e^{j\omega t}d\omega }$

توجه: در برخی از مراجع، تبدیل فوریه را به صورت زیر تعریف می کنند:

برای رزرو معلم و استاد خصوصی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

$X\left(\omega \right)=\frac{1}{\sqrt{2\pi }}\int^{+\infty }_{-\infty }{x\left(t\right).e^{-j\omega t}dt}$

و عکس آن به صورت زیر تعریف می شود:

$x\left(t\right)=\frac{1}{\sqrt{2\pi }}\int^{+\infty }_{-\infty }{X\left(\omega \right).e^{j\omega t}d\omega }$

تعریف تبدیل فوریه گسسته

تبدیل فوریه گسسته (DTFT) در برخی از مراجع به صورت زیر تعریف می شود:

$X\left(\omega \right)=\sum^{+\infty }_{n=-\infty }{x\left[n\right].e^{-j\omega n}}$

و عکس تبدیل فوریه آن به صورت زیر تعریف می شود:

$x\left[n\right]=\frac{1}{2\pi }\int^{\ }_{2\pi \ }{X\left(\omega \right).e^{j\omega n}d\omega }$

توجه: در برخی از مراجع، این تبدیل را به صورت زیر تعریف می کنند:

برای رزرو معلم و استاد خصوصی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

$X\left(\omega \right)=\frac{1}{\sqrt{2\pi }}\sum^{+\infty }_{n=-\infty }{x\left[n\right].e^{-j\omega n}}$

و عکس آن به صورت زیر تعریف می شود:

$x\left[n\right]=\frac{1}{\sqrt{2\pi }}\int^{\ }_{2\pi \ }{X\left(\omega \right).e^{j\omega n}d\omega }$

تبدیل فوریه در حوزه فرکانس | تبدیل فوریه حوزه f

در دروسی مانند درس مخابرات رشتۀ برق، تبدیل فوریه در حوزه f کاربرد دارد که تعریف آن به صورت زیر است:

$X\left(f\right)=\int^{+\infty }_{-\infty }{x\left(t\right).e^{-j2\pi ft}dt}$

و عکس تبدیل فوریه برحسب f به صورت زیر تعریف می شود:

$x\left(t\right)=\int^{+\infty }_{-\infty }{X\left(f\right).e^{j2\pi ft}df}$

تبدیل فوریه برحسب فرکانس و عکس آن، برای توابع گسسته به صورت زیر تعریف می شود:

$X\left(f\right)=\sum^{+\infty }_{n=-\infty }{x\left[n\right].e^{-j2\pi fn}}$

$x\left[n\right]=\int^{\ }_{1\ }{X\left(f\right).e^{j2\pi fn}df}$

دانلود جزوه کامل تبدیل فوریه و خواص تبدیل فوریه

در این جزوه با تعاریف، خواص و تبدیل فوریه توابع خاص پیوسته و گسسته آشنا می شوید.

دانلود جزوه کامل تبدیل فوریه

برای رزرو معلم و استاد خصوصی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

چند نکته:

1. نماد اعداد مختلط به صورت زیر تعریف می شود:

$i=j=\sqrt{-1}$

2. برای تبدیل فوریه پیوسته در حوزه w، از نمادهای زیر استفاده می کنند:

$X\left(\omega \right)=X\left(j\omega \right)$

و برای توابع گسسته نیز از نماد های زیر در مراجع مختلف استفاده می شود:

$X\left(\omega \right)=X\left(j\omega \right)=X\left(e^{j\omega }\right)$

و در حوزه f نیز این نماد ها را داریم:

$X\left(f\right)=X\left(2\pi f\right)$

3. رابطۀ اویلر را به خاطر بسپارید:

$e^{jx}={cos \left(x\right)\ }+j.{sin \left(x\right)\ }$

$e^{-jx}={cos \left(x\right)\ }-j.{sin \left(x\right)\ }$

تعریف قطار ضربه:

برای رزرو معلم و استاد خصوصی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

قطار ضربه در این درس به صورت زیر در دو حوزه w و f تعریف می شود:

$\widetilde{\delta }\left(\omega \right)=\sum^{+\infty }_{k=-\infty }{\delta (\omega -2\pi k)}$

$\widetilde{\delta }\left(f\right)=\sum^{+\infty }_{k=-\infty }{\delta (f-k)}$

توجه: به طور کلی تبدیل فوریه یک تابع مختلط است که قسمت حقیقی آن یک تابع زوج و قسمت موهوی آن یک تابع فرد است. همچنین اگر X(w) به صورت قطبی و با اندازه و زاویه بیان شود، اندازۀ آن یک تابع زوج و زاویۀ آن یک تابع فرد است.

معرفی چند تابع مهم:

1. تابع پله واحد « heavy – side »

این تابع به صورت زیر تعریف می شود:

2. تابع دلتا دیراک یا تابع ضربه:

تابع ضربه ( Dirac delta function )، به صورت زیر تعریف می شود:

3. تابع پالس « rectangle »

تابع پالس یکی از تابع های پرکابرد در این مبحث است که به صورت زیر تعریف می شود:

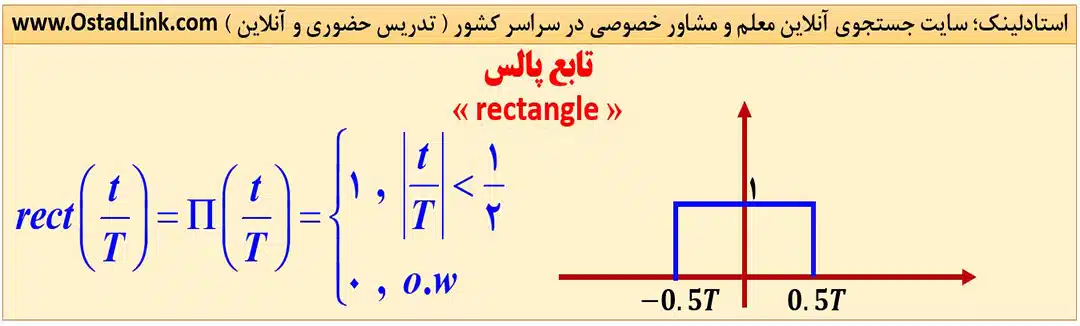
4. تابع مثلث « triangle »

این تابع به صورت زیر تعریف می شود:

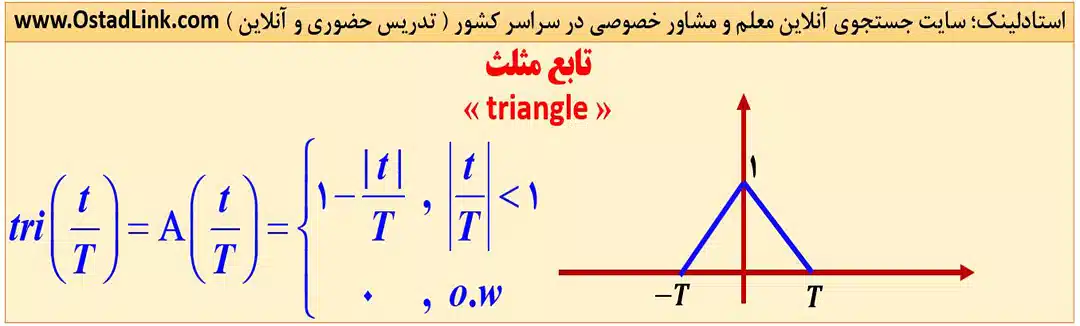
5. تابع سینک نرمال

تابع سینک نرمال به صورت زیر تعریف می شود:

برای رزرو معلم و استاد خصوصی مورد نظر خود، از طریق پشتیبانی واتساپ سایت استادلینک اقدام نمایید.

توجه: در این مقاله هر جا از تابع سینک استفاده شد، منظور تابع سینک نرمال است.

6. تابع سینک غیرنرمال

تابع سینک غیر نرمال به صورت زیر تعریف می شود:

خواص تابع سینک

برای تابع سینک (نرمال) می توان خواص زیر را در نظر گرفت که هریک از آنها، قابل اثبات هستند:

$\int^{+\infty }_{-\infty }{sinc\left(t\right)dt=1}$

$\int^{+\infty }_{-\infty }{\left|sinc\left(t\right)\right|dt=\infty }$

$\int^{+\infty }_{-\infty }{sinc^2\left(t\right)dt=1}$

$\int^{+\infty }_{-\infty }{|sinc\left(t\right){\left.{}\right|}^2dt=1}$

مقالات مرتبط:

آموزش سری فوریه و جدول خواص سری فوریه

آموزش جامع تبدیل لاپلاس و تابع گاما

آموزش انتگرال فوریه

داغ‌ترین مطالب روز

دانلود سوالات امتحان نهایی فلسفه انسانی دوازدهم شهریور 1399 + جواب

دانلود پی دی اف سوالات امتحان نهایی فلسفه 2 دوازدهم انسانی شهریور 1399 همراه با پاسخنامه تشریحی + معرفی بهترین معلم خصوصی و تدریس خصوصی ویژه امتحانات نهایی رشته انسانی در ادامه با بارم بندی امتحان نهایی فلسفه 2 رشته علوم انسانی و نحوه مطالعه صحیح این درس و راه حل پاس شدن در امتحانات […]

دانلود سوالات امتحان نهایی عربی ۳ دوازدهم تجربی و ریاضی خرداد ۱۴۰۲ + جواب

دانلود سوالات امتحان نهایی عربی 3 دوازدهم تجربی و ریاضی خرداد 1402 همراه با پاسخنامه تشریحی + معرفی بهترین معلم خصوصی و تدریس خصوصی ویژه امتحانات نهایی رشته تجربی و ریاضی در ادامه با بارم بندی امتحان نهایی عربی رشته تجربی و ریاضی و نحوه مطالعه صحیح این درس و راه حل پاس شدن در […]

دانلود سوالات آزمون 22 تیر 1402 ماز تمامی رشته ها با پاسخنامه تشریحی

دانلود رایگان آزمون آزمایشی 22 تیر 1402 ماز ( بیوماز ) به همراه پاسخنامه تشریحی تمامی رشته ها ( دهم، یازدهم و دوازدهم رشته های ریاضی، تجربی و انسانی ) توجه: گردآوری مطالب این بخش توسط تیم سایت تدریس خصوصی استادلینک انجام شده و استفاده از مطالب آن با ذکر نام منبع ( سایت استاد لینک […]