در این مقاله قسط داریم که آموزش جامع فرمول های تبدیل لاپلاس و تابع گاما از سری مباحث مهم درس معادلات دیفرانسیل را به شما عزیزان توسط اساتید ریاضی سایت استادلینک آموزش دهیم.
استادلینک؛ جامع ترین وبسایت جستجوی استاد خصوصی ریاضی در سراسر کشور است که می توانید رزومۀ بهترین اساتید را در آن مشاهده نمایید. در ادامه با آموزش جامع تبدیل لاپلاس و تابع گاما همراه خواهید بود و جزوۀ کامل تبدیل لاپلاس قابل دانلود می باشد.
آنچه در این مقاله می‌خوانید
بهترین استاد ریاضیات دانشگاهی در اصفهان
برای رزرو کلاس های خصوصی آنلاین و حضوری ریاضیات دانشگاهی مهندس امید نجفی پور می توانید با شماره 09130394201 آکادمی نجفی تماس حاصل نمایید.
مرکز مشاوره درسی تحصیلی آکادمی نجفی
گروه آموزشی و مشاوره و برنامه ریزی تحصیلی و درسی
شماره تماس : 09130394201
نظرات دانش آموزان
آدرس: فلکه احمدآباد – خیابان جی – نرسیده به چهارراه پروین – کوچه ظفر (21)
تعریف تبدیل لاپلاس یکطرفه
تبدیلات ریاضی برای این به وجود آمده اند، که عملیات های پیچیده را ساده تر کنند. تبدیل لاپلاس هم یکی از انواع تبدیل های ریاضی مانند تبدیل فوریه، تبدیل z و … می باشد.
این تبدیل ها از جمله لاپلاس، در مهندسی گوناگونی مانند رشتۀ برق، برای حل معادلات دیفرانسیل به کار می آیند. در قسمت زیر فرمول تبدیل لاپلاس یکطرفه را مشاهده می کنید.
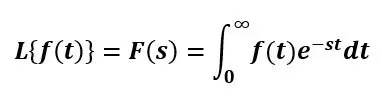
که داریم:
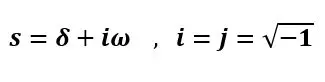
شرط همگرایی تبدیل لاپلاس یک طرفه این است که قسمت حقیقی s، مثبت باشد یعنی:
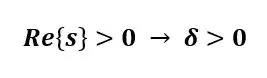
فرمول های کامل تبدیل لاپلاس
در تصویر زیر، تمامی روابط مهم در تبدیل لاپلاس، به نمایش داده شده است.
جهت رزرو استاد خصوصی درس معادلات دیفرانسیل به آموزشگاه آکادمی نجفی پیام دهید.
تماس
تلگرام
واتساپ
ایتا1- خاصیت خطی بودن
این خاصیت جمع پذیری و همگن بودن لاپلاس را بیان می کند.
2- تغییر مقیاس زمانی
اگر زمان در عددی ضرب شود، s و مقدار کلی تابع تبدیل لاپلاس در معکوس آن عدد ضرب می شود.
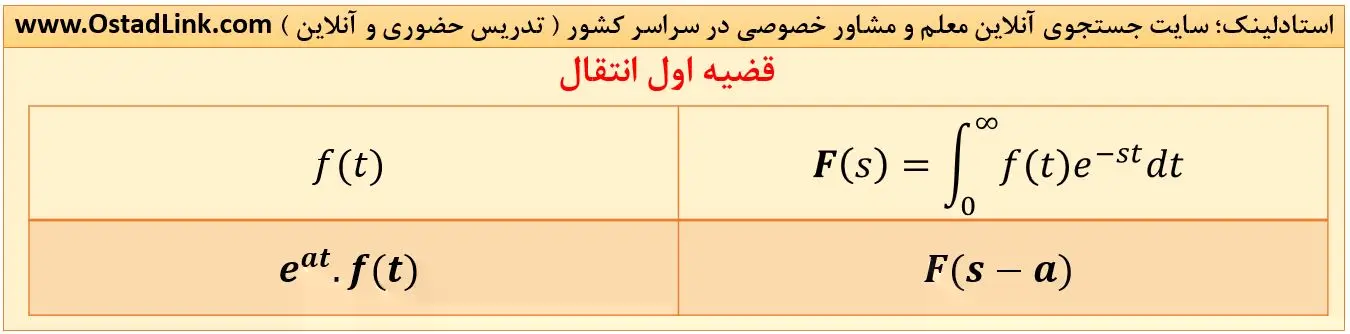
3- قضیه اول انتقال
تابع نمایی باعث انتقال در حوزۀ لاپلاس می شود.
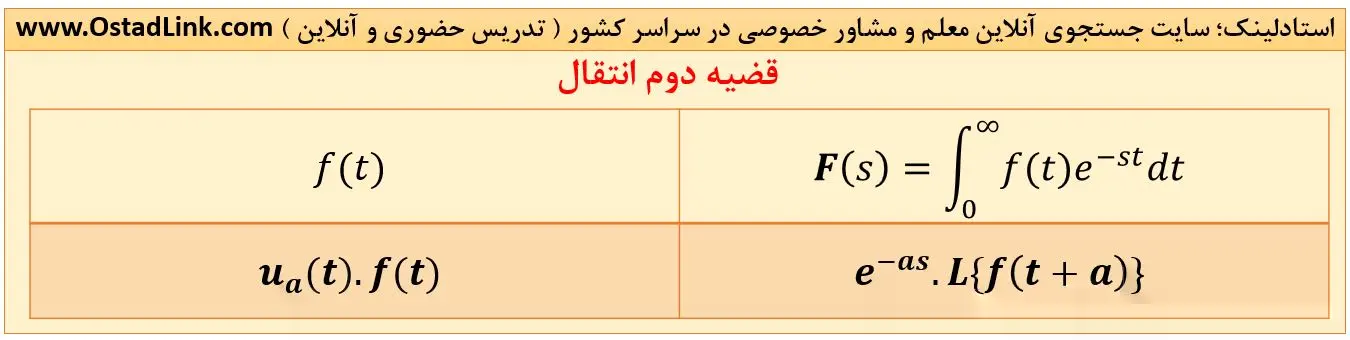
4- قضیه دوم انتقال
منظور از ua(t) همان تابع پله یا هویساید ( heavy-side ) می باشد که باعث تاخیر در مقدار دهی به تابع f(t) می شود. این عمل باعث میشود که در حوزۀ لاپلاس تابع نمایی ایجاد شود که در درس کنترل خطی بسیار حائز اهمیت است.
![\[{\boldsymbol{u}}_{\boldsymbol{a}}\left(\boldsymbol{t}\right)\boldsymbol{=}\boldsymbol{u}\boldsymbol{(}\boldsymbol{t}\boldsymbol{-}\boldsymbol{a}\boldsymbol{)}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-218513721d04c435e95a3e20f0bc9515_l3.png "Rendered by QuickLaTeX.com")
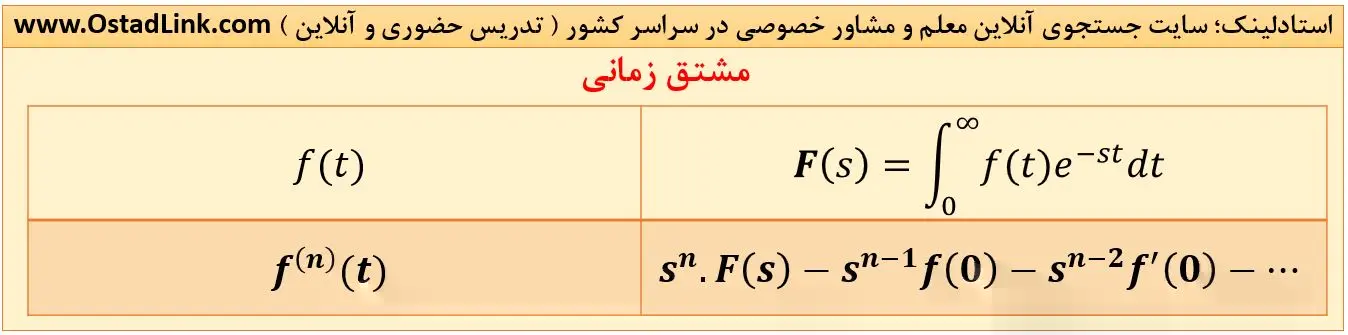
5- مشتق در حوزۀ زمان
اپراتور s در حوزۀ لاپلاس به معنای مشتق مرتبۀ اول در حوزۀ زمان است. همچنین sn به معنای مشتق مرتبۀ n اُم در حوزۀ زمان است. همچنین f(0) و f'(0) و ….. شرایط اولیه در حوزۀ زمان می باشد.
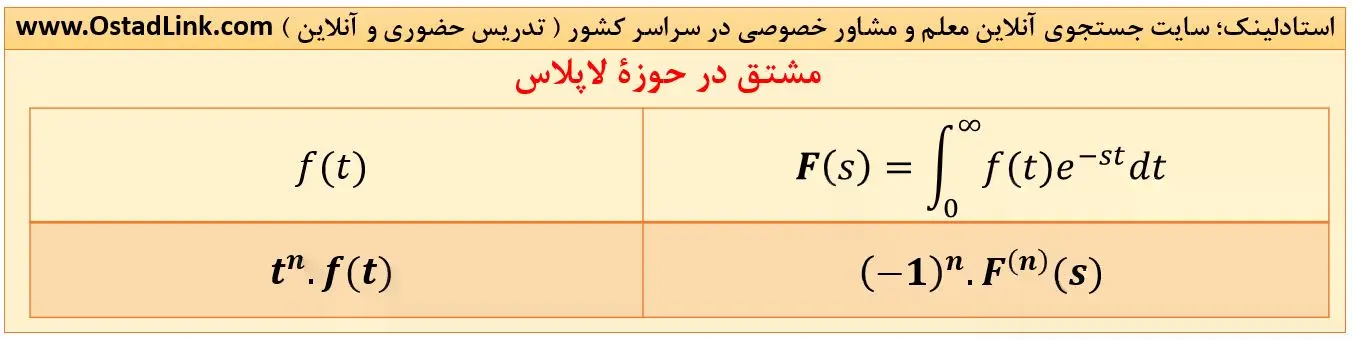
6- مشتق در حوزه لاپلاس
ضرب t در حوزۀ زمان باعث ایجاد مشتق در حوزۀ لاپلاس می شود.
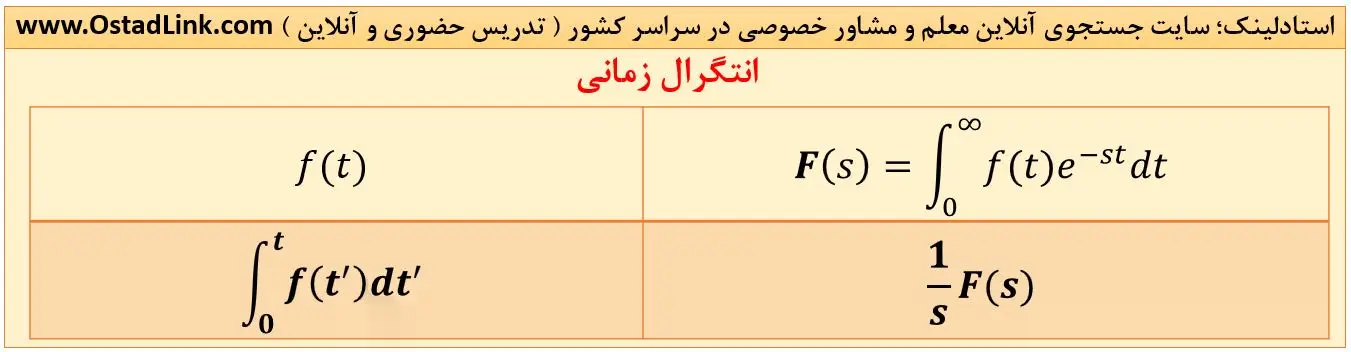
7- انتگرال در حوزۀ زمان
همانطور که گفته شد s در حوزۀ لاپلاس به معنای مشتق در حوزۀ زمان می باشد. همانطور که می دانیم مشتق و انتگرال دو عملیات معکوس هم هستند. پس معکوس s به معنای انتگرال در حوزۀ زمان می باشد.
8- انتگرال در حوزۀ لاپلاس
همانطور که ضرب t در تابع در حوزۀ زمان، باعث مشتق در حوزۀ لاپلاس می شود، تقسیم t نیر در حوزۀ زمان، باعث ایجاد انتگرال در حوزۀ لاپلاس می شود.
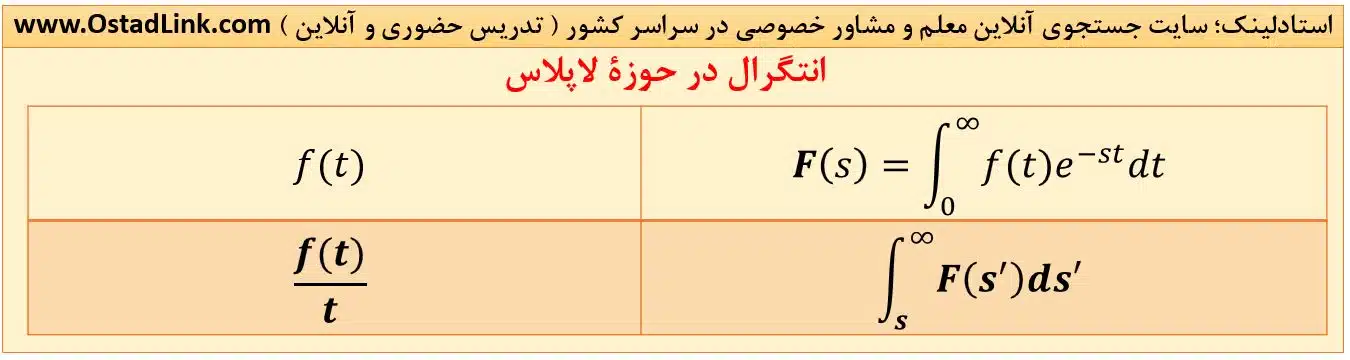
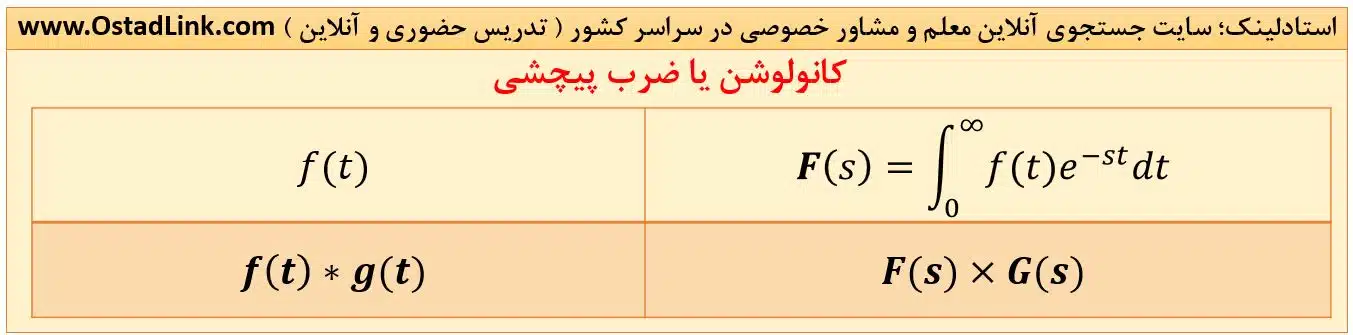
9- کانولوشن یا ضرب پیچشی
تعریف کانولوشن یا ضرب پیچشی را در ادامه خواهید دید که یک عملیات پیچیده در ریاضی محسوب می شود. این عملیات پیچیده توسط لاپلاس به یک عملیات سادۀ ضرب تبدیل می شود.
در مهندسی برق، در سیستم های LTI ( خطی تغییر ناپذیر با زمان )، خروجی از کانولوشن ورودی و تابع انتقال بدست می آید که با استفاده از تبدیل لاپلاس، به عملیات سادۀ ضرب تبدیل می شود.
10- ضرب در حوزۀ زمان
طبق خاصیت دوگانگی (Duality) که در ادامه به آن میپردازیم، ضرب دو تابع در حوزۀ زمان، باعث ایجاد کانولوشن در حوزۀ لاپلاس می شود.
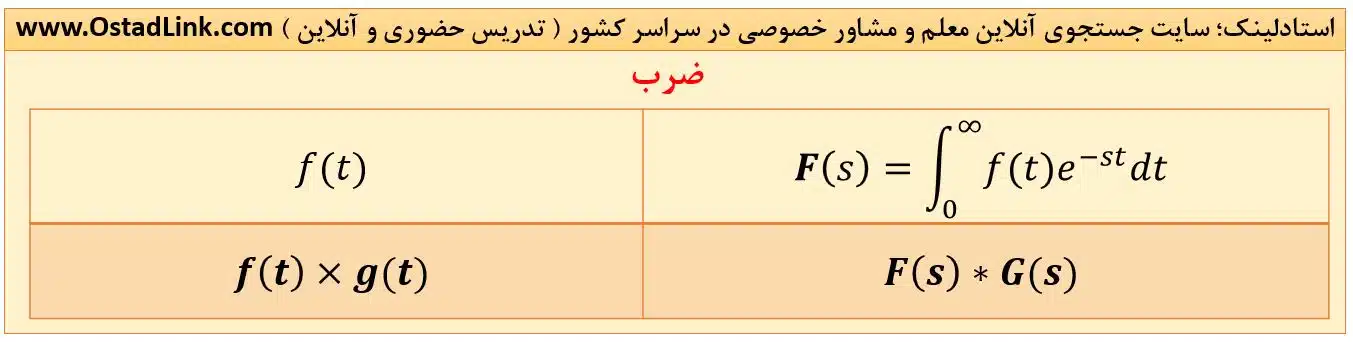
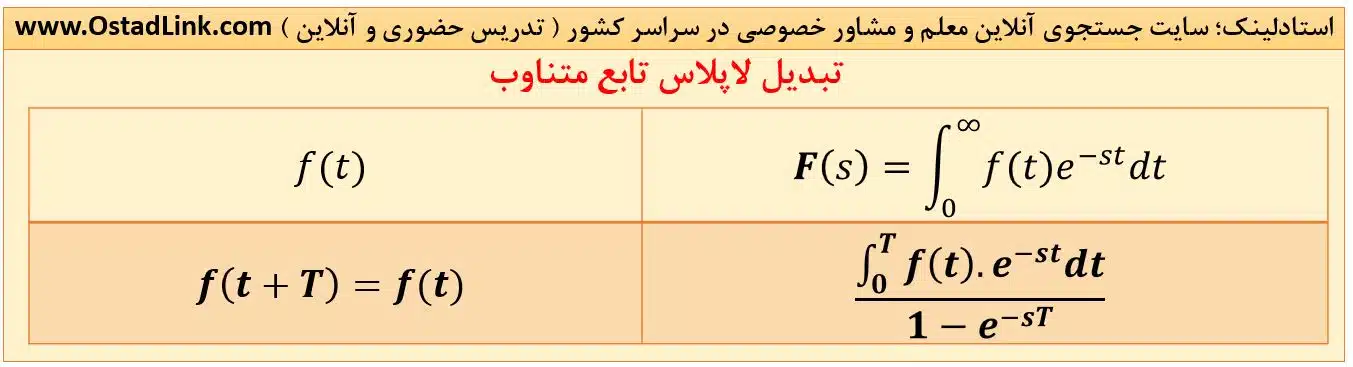
11- لاپلاس تابع متناوب
برای تابع متناوب f(t) با دورۀ تناوب T داریم:
12- قضیه مقدار اولیه
اگر مقدار اولیه تابع f(t) در حوزه زمان در t=0 احتیاج باشد ولی F(s) موجود باشد، از رابطۀ زیر استفاده می کنیم.
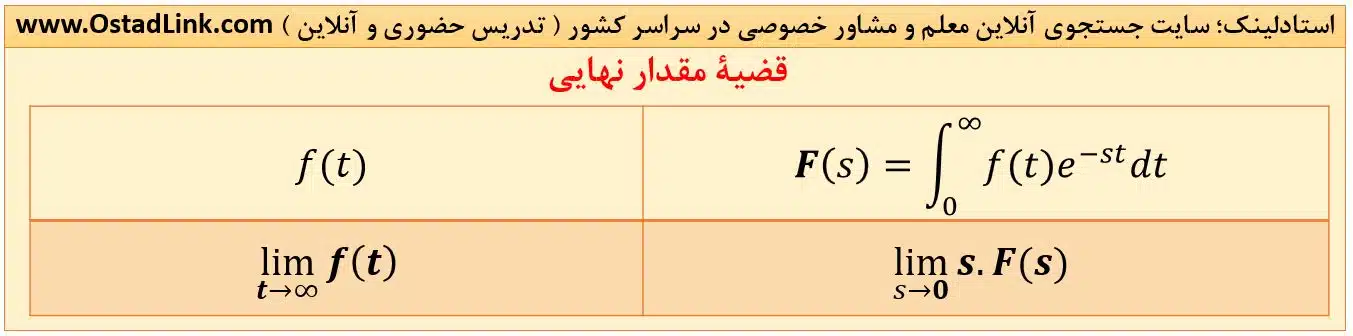
13- قضیه مقدار نهایی
اگر تابع F(s) پایدار و دارای قطب منفی باشد، می توان از رابطۀ زیر مقدار نهایی تابع را در زمان بی نهایت در حوزۀ زمان بدست آورد.
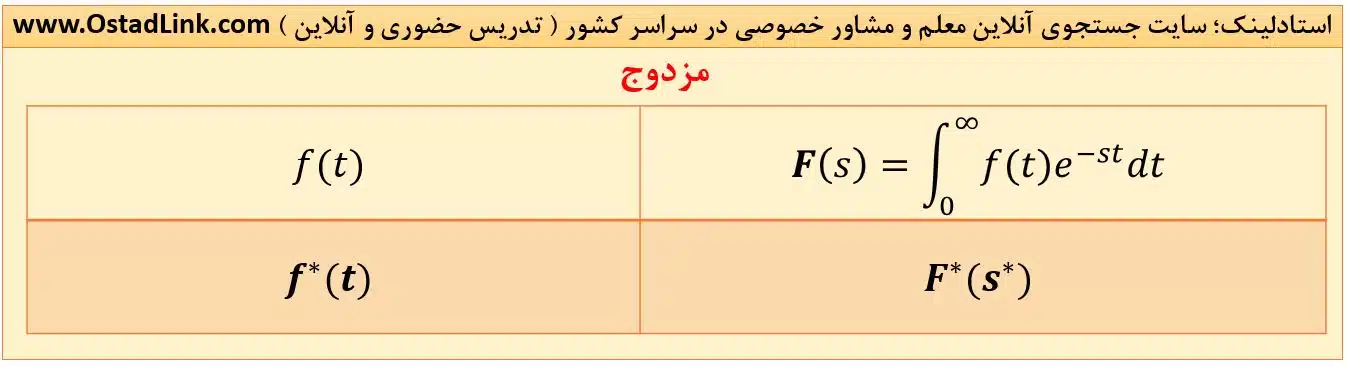
14- مزدوج
مزدوج یک تابع در حوزۀ زمان باعث مزدوج شدن اپراتور s و کل جواب در حوزۀ لاپلاس می شود.
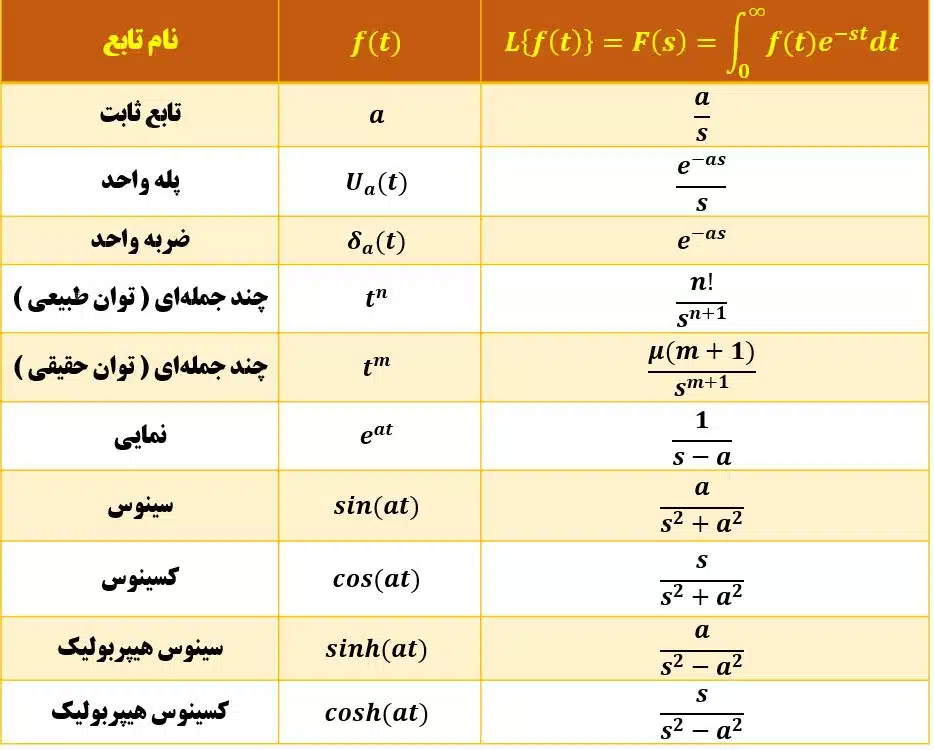
تبدیل لاپلاس توابع خاص
در قسمت قبل، با خواص لاپلاس در حالت های گوناگون قرار گرفتن تابع f(t) آشنا شدید. در این قسمت، لاپلاس توابع خواص که حتماً باید آنها را به خاطر بسپارید، برای شما آمده است.
جهت رزرو استاد خصوصی درس معادلات دیفرانسیل به پشتیبانی واتساپ سایت استادلینک پیام دهید.
معرفی تابع پله، ضربه و توابع هذلولوی
1- تابع پله
تابع پله، به ازای مقادیر مثبت و صفر داخل آن، برابر یک و به ازای مقادیر منفی داخل آن، برابر صفر است. نمودارو روابط تابع پله به صورت زیر می باشد.
2- تابع ضربه
تابع ضربه (impulse)، مشتق تابع پله است که در مهندسی های گوناگون از جمله مهندسی برق، بسیار کاربرد دارد.
3- توابع هذلولوی (Hyperbolic)
تابع سینوس هیپربولیک و کسینوس هیپربولیک به صورت زیر تعریف می شود:
ضرب پیچشی یا کانولوشن
برای دو تابع f(t) و g(t)، کانولوشن یا ضرب پیچشی به صورت زیر تعریف می شود.
![\[f\left(t\right)*g\left(t\right)=\int^{+\infty }_{-\infty }{f\left(k\right).g\left(t-k\right)dk}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-28579a2275898ce33dde4031b509b6b9_l3.png "Rendered by QuickLaTeX.com")
اگر دو تابع f(t) و g(t) برای زمانهای مثبت تعریف شده باشند داریم:
![\[f\left(t\right)*g\left(t\right)=\int^t_0{f\left(k\right).g\left(t-k\right)dk}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-b331a0a52640047367fe18b9e7f87b1d_l3.png "Rendered by QuickLaTeX.com")
خواص کانولوشن
برای ضرب پیچشی یا کانولوشن می توان خواص زیر را تعیین کرد.
تابع گاما
این تابع به صورت زیر تعریف می شود:
![\[\boldsymbol{\mu }\left(\boldsymbol{m}\boldsymbol{+}\boldsymbol{1}\right)\boldsymbol{=}\int^{\boldsymbol{m}}_{\boldsymbol{0}}{{\boldsymbol{x}}^{\boldsymbol{m}}.{\boldsymbol{e}}^{\boldsymbol{-}\boldsymbol{t}}\boldsymbol{dt}}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-2b2b2497161c432f815c9b78d4eb5c0d_l3.png "Rendered by QuickLaTeX.com")
جهت رزرو استاد خصوصی درس معادلات دیفرانسیل به آموزشگاه آکادمی نجفی پیام دهید.
قواعد تابع گاما
1- برای هر عدد حقیقی m داریم:
![\[\boldsymbol{\mu }\left(\boldsymbol{m}\boldsymbol{+}\boldsymbol{1}\right)\boldsymbol{=}\boldsymbol{m}.\boldsymbol{\mu }\boldsymbol{(}\boldsymbol{m}\boldsymbol{)}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-2edea40effdccf323c63be8f187e55fa_l3.png "Rendered by QuickLaTeX.com")
2- برای عدد طبیعی n رابطۀ بالا به صورت زیر اصلاح می شود: ( فاکتوریل اعداد کسری و منفی را می توان به کمک این تابع بدست آورد )
![\[\boldsymbol{\mu }\left(\boldsymbol{n}\boldsymbol{+}\boldsymbol{1}\right)\boldsymbol{=}\boldsymbol{n}\boldsymbol{!}~~~\boldsymbol{(}\boldsymbol{n}\boldsymbol{\in }\mathbb{N}\mathrm{)}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-24264cb319fe91973b7524d36d173dcb_l3.png "Rendered by QuickLaTeX.com")
3- رابطۀ زیر قابل اثبات است:
![\[\boldsymbol{\mu }\left(\boldsymbol{m}\right).\boldsymbol{\mu }\left(\boldsymbol{1}\boldsymbol{-}\boldsymbol{m}\right)\boldsymbol{=}\frac{\boldsymbol{\pi }}{\boldsymbol{sin}\boldsymbol{(}\boldsymbol{\pi }\boldsymbol{m}\boldsymbol{)}}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-0f303ad501631cde8b4b4442242d9954_l3.png "Rendered by QuickLaTeX.com")
4- برای هر عدد طبیعی n داریم:
![\[\boldsymbol{\mu }\left(\frac{\boldsymbol{1}}{\boldsymbol{2}}\right)\boldsymbol{=}\sqrt{\boldsymbol{\pi }}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-d04c59e772a745f028aed5ff1b03d05e_l3.png "Rendered by QuickLaTeX.com")
![\[\boldsymbol{\mu }\left(\boldsymbol{n}\boldsymbol{+}\frac{\boldsymbol{1}}{\boldsymbol{2}}\right)\boldsymbol{=}\frac{\boldsymbol{1}\boldsymbol{\times }\boldsymbol{3}\boldsymbol{\times \dots \times (}\boldsymbol{2}\boldsymbol{n}\boldsymbol{-}\boldsymbol{1}\boldsymbol{)}}{{\boldsymbol{2}}^{\boldsymbol{n}}}\boldsymbol{\times }\sqrt{\boldsymbol{\pi }}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-48daa0dd1f60894398a2a2bc073e9c3f_l3.png "Rendered by QuickLaTeX.com")
![\[\boldsymbol{\mu }\left(\boldsymbol{-}\boldsymbol{n}\boldsymbol{+}\frac{\boldsymbol{1}}{\boldsymbol{2}}\right)\boldsymbol{=}\frac{{\left(\boldsymbol{-}\boldsymbol{2}\right)}^{\boldsymbol{n}}\boldsymbol{\times }\sqrt{\boldsymbol{\pi }}}{\boldsymbol{1}\boldsymbol{\times }\boldsymbol{3}\boldsymbol{\times \dots \times (}\boldsymbol{2}\boldsymbol{n}\boldsymbol{-}\boldsymbol{1}\boldsymbol{)}}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-97d2c921ee52b76d083e4234af89ef54_l3.png "Rendered by QuickLaTeX.com")
چند رابطۀ مهم ریاضی
1- تبدیل ضرب به جمع توابع مثلثاتی
![\[\boldsymbol{sin}\left(\boldsymbol{\alpha }\right).\boldsymbol{cos}\left(\boldsymbol{\beta }\right)\boldsymbol{=}\frac{\boldsymbol{1}}{\boldsymbol{2}}\left[\boldsymbol{sin}\left(\boldsymbol{\alpha }\boldsymbol{-}\boldsymbol{\beta }\right)\boldsymbol{+}\boldsymbol{sin}\left(\boldsymbol{\alpha }\boldsymbol{+}\boldsymbol{\beta }\right)\right]\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-2f69a6169b21f166d100f963e510221c_l3.png "Rendered by QuickLaTeX.com")
![\[\boldsymbol{cos}\boldsymbol{(}\boldsymbol{\alpha }\boldsymbol{)}.\boldsymbol{cos}\left(\boldsymbol{\beta }\right)\boldsymbol{=}\frac{\boldsymbol{1}}{\boldsymbol{2}}\left[\boldsymbol{cos}\left(\boldsymbol{\alpha }\boldsymbol{-}\boldsymbol{\beta }\right)\boldsymbol{+}\boldsymbol{c}\boldsymbol{os}\left(\boldsymbol{\alpha }\boldsymbol{+}\boldsymbol{\beta }\right)\right]\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-3d35e0850021dbb1a6cc0bf537775a0e_l3.png "Rendered by QuickLaTeX.com")
![\[\boldsymbol{sin}\boldsymbol{(}\boldsymbol{\alpha }\boldsymbol{)}.\boldsymbol{sin}\left(\boldsymbol{\beta }\right)\boldsymbol{=}\frac{\boldsymbol{1}}{\boldsymbol{2}}\left[\boldsymbol{cos}\left(\boldsymbol{\alpha }\boldsymbol{-}\boldsymbol{\beta }\right)\boldsymbol{-}\boldsymbol{c}\boldsymbol{os}\left(\boldsymbol{\alpha }\boldsymbol{+}\boldsymbol{\beta }\right)\right]\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-015fb70cd8efeac9937c454d8d777391_l3.png "Rendered by QuickLaTeX.com")
2- رابطۀ طلایی در مثلثات
![\[{\boldsymbol{cos}}^{\boldsymbol{2}}\left(\boldsymbol{\alpha }\right)\boldsymbol{=}\frac{\boldsymbol{1}}{\boldsymbol{2}}\boldsymbol{+}\frac{\boldsymbol{1}}{\boldsymbol{2}}\boldsymbol{cos}\boldsymbol{(}\boldsymbol{2}\boldsymbol{\alpha }\boldsymbol{)}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-69b9c81dde03707a2dcd45b9372712cb_l3.png "Rendered by QuickLaTeX.com")
![\[{\boldsymbol{sin}}^{\boldsymbol{2}}\left(\boldsymbol{\alpha }\right)\boldsymbol{=}\frac{\boldsymbol{1}}{\boldsymbol{2}}\boldsymbol{-}\frac{\boldsymbol{1}}{\boldsymbol{2}}\boldsymbol{cos}\boldsymbol{(}\boldsymbol{2}\boldsymbol{\alpha }\boldsymbol{)}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-f6256eb259e93907339722f324636945_l3.png "Rendered by QuickLaTeX.com")
3- رابطۀ طلایی در توابع نمایی
از این رابطه برای لاپلاس معکوس گرفتن، بسیار استفاده می شود.
![\[{\boldsymbol{a}}^{\boldsymbol{s}}\boldsymbol{=}{\boldsymbol{e}}^{\boldsymbol{Ln}\left(\boldsymbol{a}\right).\boldsymbol{s}}\]](https://ostadlink.com/mag/wp-content/ql-cache/quicklatex.com-ad7de9f4290e169b364ad8a473aeb21a_l3.png "Rendered by QuickLaTeX.com")
دانلود جزوه کامل تبدیل لاپلاس
برای دانلود جزوه کامل تبدیل لاپلاس، روی جعبۀ زیر ضربه بزنید.
جهت رزرو استاد خصوصی درس معادلات دیفرانسیل به آموزشگاه آکادمی نجفی پیام دهید.
“This gives the transform many applications in science and engineering, mostly as a tool for solving linear differential equations and dynamical systems by simplifying ordinary differential equations and integral equations into algebraic polynomial equations, and by simplifying convolution into multiplication.”
«تبدیل لاپلاس، کاربردهای فراوانی برای این تبدیل در علم و مهندسی ایجاد می‌کند؛ عمدتاً به‌عنوان ابزاری برای حل معادلات دیفرانسیل خطی و سیستم‌های دینامیکی، از طریق ساده‌کردن معادلات دیفرانسیل معمولی و معادلات انتگرالی به معادلات جبری چندجمله‌ای، و همچنین ساده‌کردن پیچیدگی کانولوشن به ضرب.»
منبع: ویکی پدیا
مقالات مرتبط:
دانلود تمامی فرمول های مشتق (جدول های مشتق)